Assessing the performance of Vienna Mapping Functions 3 for GNSS stations in Indonesia using Precise Point Positioning
Nabila Putri
Daniel Landskron
Johannes Böhm
Tropospheric delay is one of the major error sources for space geodetic techniques, such as the Global Navigation Satellite Systems (GNSS). Mapping functions are used to scale the delay from zenith direction to the elevation angle of the signal. Several mapping functions have already been published, including the Global Mapping Functions (GMF) and Vienna Mapping Functions 1 (VMF1). Recently, a refined version of VMF1, VMF3, was released. The tropospheric gradients GRAD were also determined using the same data set as VMF3. This study aims to test the performance of VMF3 on GNSS observations in Indonesia, using observations from 21 stations of the permanent GNSS network in Indonesia, InaCORS. Data processing was carried out using Precise Point Positioning in Bernese GNSS Software, version 5.2 for the year 2014. Station coordinates were estimated daily, while the zenith wet delays were estimated every 30 min and tropospheric gradients were estimated hourly. A similar processing scheme was carried out using GMF and VMF1. Generally, the results from VMF3 agree very well with the results from GMF and VMF1, although small biases can be found, especially for the height component. Based on the repeatability, while there is no significant difference for the latitude and longitude, there are slight improvements for the height, particularly compared to GMF. The estimated gradients tend to fluctuate more compared to gradients from GRAD. The correlation coefficients between the estimated gradients and those from GRAD are small, with the largest being 0.65 at site CUKE.
Tropospheric delay is one of the major error sources in space geodetic observations. It needs to be taken into account during the analysis to improve the quality of observation model. Generally, tropospheric delays can be divided into two components: the hydrostatic and wet delays. These delays are often described as the delays at the zenith direction.
Zenith hydrostatic delays can be obtained using surface pressure measurements at the station. Several models have been developed to calculate , for instance the model by Saastamoinen (1972):
where p is pressure, φ is geographic latitude, and hell is ellipsoidal height of the site.
Zenith wet delays depend on the amount of water vapor in the atmosphere. Since water vapor is highly variable, temporally and spatially, it is more difficult to estimate based only on surface measurements. It is common practice to estimate along with other parameters during the analysis of GNSS observations. Alternatively, it is also possible to approximate using various models, such as using the formula by Askne and Nordius (1987):
where and k3 are empirically determined refractivity constants, Rd is the specific gas constant for dry constituents, and gm is the mean gravity. This formula requires information on water vapor pressure e, mean temperature weighted with water vapor pressure Tm, and water vapor decrease factor λ.
Mapping functions are then used to scale the tropospheric delays from the zenith direction down to the elevation angle of the signal. Several mapping functions have already been published, for instance the Global Mapping Functions, GMF (Böhm et al., 2006a), and the Vienna Mapping Functions 1, VMF1 (Böhm et al., 2006b). Recently, a refined version of VMF1, VMF3 (Landskron and Böhm, 2017), was released.
VMF3 was developed based on ray-traced delays using data from the European Centre for Medium-Range Weather Forecasts (ECMWF), ERA-Interim, from the year 2001 to 2010, at 3∘ elevation angle (for grid) and eight azimuth angles (). The coefficients a, b, and c were determined using least-squares adjustment. The b and c coefficients have a temporal and spatial dependence, which was accomplished by estimating seasonal fits containing annual and semi-annual terms for the temporal dependence, and using a spherical harmonics expansion up to degree 12 for the spatial dependence.
Tropospheric horizontal gradients also need to be considered to account for azimuthal asymmetry, especially for observations at low elevation angles. Horizontal gradients can be estimated in the analysis of GNSS or Very Long Baseline Interferometry (VLBI) observations. However, it is also possible to obtain these gradients from other sources, such as from Numerical Weather Models (NWMs). The tropospheric gradients GRAD (Landskron and Böhm, 2018) were determined through ray-tracing using the same NWMs as VMF3, based on the model by Chen and Herring (1997):
where Gn and Ge are the north and east gradients, respectively, and mfg is the gradients mapping function. ΔL0 is the product of the zenith hydrostatic and wet delays with their respective mapping functions (the isotropic part):
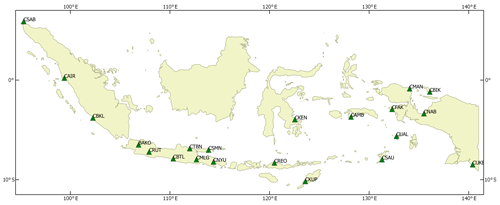
This study aims to assess the performance of VMF3 on GNSS observations in Indonesia. For this purpose, 21 stations from the Indonesian permanent GNSS network, InaCORS, were chosen based on their location and data availability. The map of the stations can be seen in Fig. 1. The majority of InaCORS stations are located on Java Island. Most stations on other islands were constructed recently and therefore have limited number of observations.
Data processing was carried out using Precise Point Positioning (PPP) in Bernese GNSS Software 5.2 (Dach et al., 2015) for the year 2014. The elevation cutoff angle is 5∘, while the antenna corrections, orbit files, and clock corrections are taken from the Center for Orbit Determination in Europe, CODE (Dach et al., 2016). Three different mapping functions were used, namely GMF, VMF1, and VMF3. Since Bernese only supports GMF and VMF1, changes had to be made in the Bernese subroutines in order to allow the software to use VMF3. The codes for VMF3 can be found at http://vmf.geo.tuwien.ac.at/codes/ (last access: 4 March 2020).
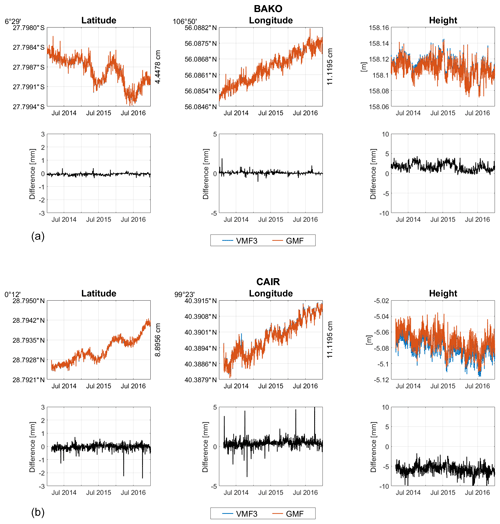
Figure 2Estimated coordinates from VMF3 and GMF and their differences for station BAKO (a) and CAIR (b). On the right side of the latitude and longitude plot, max-min value in cm is given.
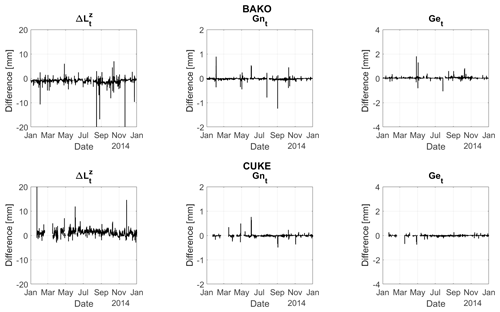
Figure 3The differences of tropospheric parameters from VMF3 and GMF. Zenith wet delays and gradients (north and south) were estimated.
The comparison of estimated coordinates and tropospheric parameters from VMF3 and GMF is shown in Sect. 2, while the comparison with VMF1 is shown in Sect. 3. The slant tropospheric delays at 5∘ elevation angle from all three mapping functions are shown in Sect. 4. Section 5 presents the comparison of the estimated gradients using VMF3 with the gradients from the model GRAD. Conclusions are drawn in Sect. 6.
The first analysis was carried out using VMF3 troposphere model, specifically the gridded version, since none of the InaCORS stations are part of the IGS network (with the exception of site BAKO). The a priori hydrostatic zenith delays were also taken from the gridded VMF3. Gridded VMF3 is available in two grid sizes: and resolutions. For this study, the 1∘ version was chosen since it has higher resolution than VMF1.
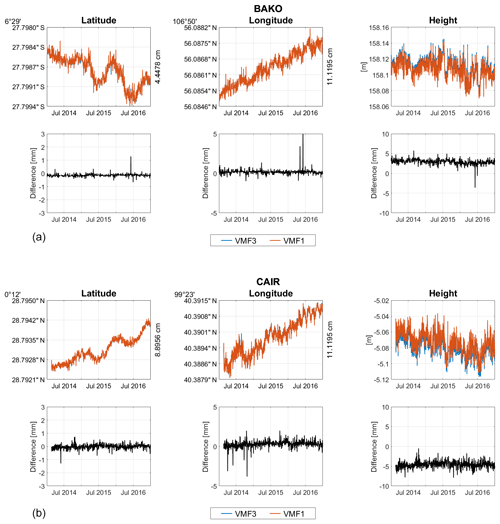
Figure 5Estimated coordinates from VMF3 and VMF1 and their differences for station BAKO (a) and CAIR (b). On the right side of the latitude and longitude plot, max-min value in cm is given.
Station coordinates were estimated daily, while zenith wet delays were estimated every 30 min, and tropospheric gradients (both north and east) were estimated hourly. The results were then compared with GMF whose a priori were based on the values of the Global Pressure and Temperature, GPT (Böhm et al., 2007). The estimated coordinates comparison as well as the differences at two stations are shown in Fig. 2, namely at stations BAKO in West Java and CAIR in West Sumatra. BAKO was chosen since it is part of the IGS network, while CAIR since it is located almost at the equator.
Both results, from VMF3 and GMF processing schemes, agree very well at all stations, particularly for the horizontal components. The differences in the estimated latitude and longitude are typically smaller than 1 mm, with the longitude differences slightly larger than the latitude. At some stations, small biases appear in the height component, similar to site CAIR (Fig. 2, lower part). However, in general, the estimated heights from VMF3 and GMF agree well. The differences between the two models for the height component are at the mm level.
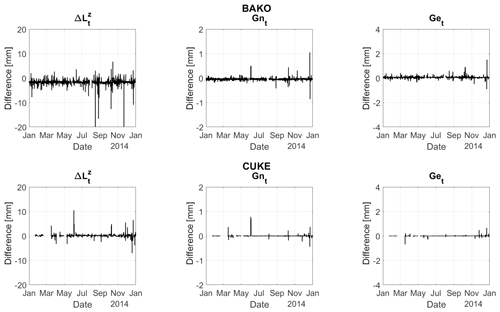
Figure 6The differences of tropospheric parameters from VMF3 and VMF1. Zenith wet delays and gradients (north and south) were estimated.
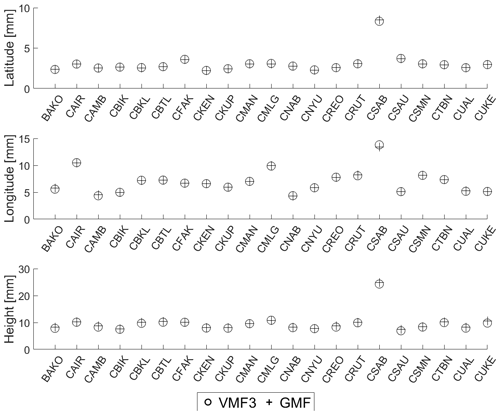
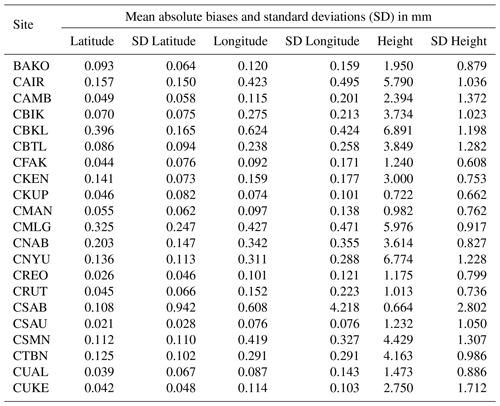
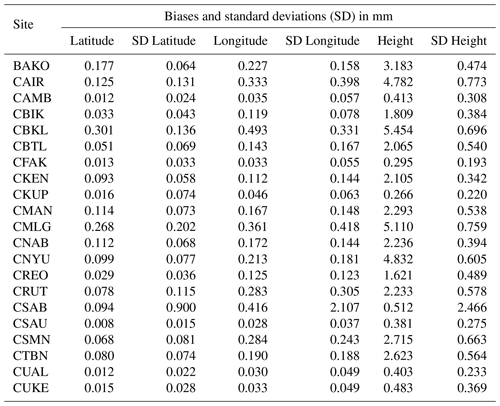
The mean absolute biases and the standard deviations for all 21 sites can be seen in Table 1. For latitude and longitude, the mean biases are smaller than 1 mm, whereas for the height, the mean absolute biases range from less than 1 mm (at station CKUP) to more than 6 mm (at station CBKL).
Additionally, tropospheric parameters are also compared, namely the zenith total delays and total tropospheric gradients (north and east), Gnt and Get, respectively. The comparison of the differences between the tropospheric estimates can be seen in Fig. 3. The differences between the estimated from both models are less than 1 cm with a SD of around 0.6 mm. For the estimated gradients, the differences are typically less than 2 mm with a SD of less than 0.1 mm, although the values for Get are larger than Gnt.
To compare the performance between VMF3 and GMF, the repeatability of the estimated coordinates from each station was determined. The comparison can be seen in Fig. 4. In general, both VMF3 and GMF yield similar results. This is especially true for the horizontal components, latitude and longitude. However, for the height component, using VMF3 yields slightly better results for more than half of the stations, as seen from smaller standard deviations.
The second comparison was done for VMF3 and VMF1, which are both discrete mapping functions. For VMF1, the a priori were taken from the gridded VMF1, which is available for the grid size . VMF3 and its a priori were taken from the grid size, similar to Sect. 2.
The comparison of estimated coordinates and their differences at sites BAKO and CAIR can be seen in Fig. 5. The differences between VMF3-VMF1 are generally smaller than VMF3-GMF at all sites, probably because both are discrete mapping functions, whereas GMF is empirical. Small biases of a few mm also appear in the height component, as with GMF, only to a smaller degree.
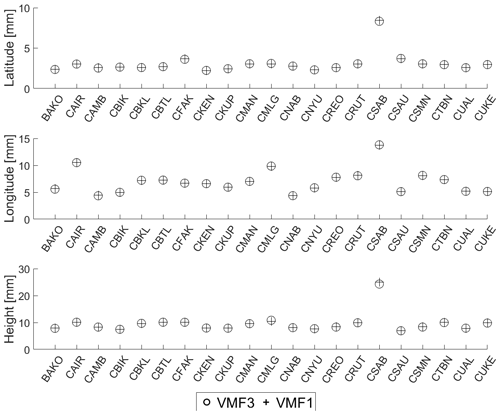
The mean absolute biases and the standard deviations can be seen in Table 2. Compared to GMF, the biases for VMF1 are generally smaller. This is especially obvious for the height component.
The differences in tropospheric estimates (, Gnt, and Get) can be seen in Fig. 6. The results are quite similar as the differences between tropospheric estimates from VMF3-GMF.
The repeatability of the estimated coordinates from VMF3 and VMF1 are depicted in Fig. 7. The results from VMF3 and VMF1 are very similar for all three components. The height components at some sites are slightly improved when using VMF3.
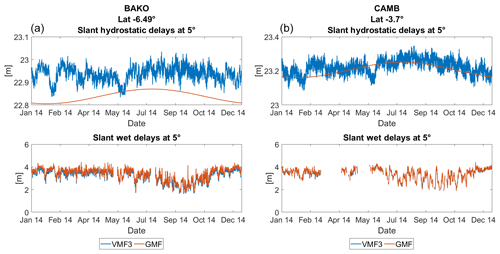
Slant delays at 5∘ were calculated using VMF3, VMF1, and GMF. In the case of VMF3 and VMF1, a priori zenith hydrostatic delay was based on the ECMWF re-analysis data using Eq. (1). For GMF, a priori was computed based on the values from the Global Pressure and Temperature, GPT (Böhm et al., 2007).
The comparison of slant delays at two sites from VMF3 and GMF can be seen in Fig. 8. While a seasonal pattern is clear for ΔLh from GMF, such pattern is not very visible in the case of VMF3 for most sites. However, the seasonal pattern is more visible for the estimated slant wet delays ΔLw. This might be due to the fact that Indonesia's climate is mainly characterized by changes in rainfall, instead of temperature and pressure. The variation in rainfall is due to the monsoon patterns, whose changes in directions correspond to the dry season and the rainy season. For regions located in the south of equator, the dry season occurs from June to October and rainy season from November to March. For regions located in the north of equator, the opposite is the case. Closer to the equator, the amount of rainfall throughout the year does not vary significantly.
ΔLh at site BAKO from GMF is smaller than from VMF3 (Fig. 8, left side). This is also the case at some other sites. However, for most other sites, including site CAMB (Fig. 8, right side), ΔLh from VMF3 agrees well with ΔLh from GMF.
Seasonal patterns can be seen in ΔLw for sites BAKO. ΔLw is smaller between May and November, which coincides with the middle of the dry season until the beginning of the rainy season in Indonesia. Generally, seasonal patterns are more obvious at sites located farther away from the equator. However, for sites located in the eastern part of Indonesia, in Papua and on the islands of Maluku (e.g. site CAMB), the seasonal pattern for ΔLw is not visible.
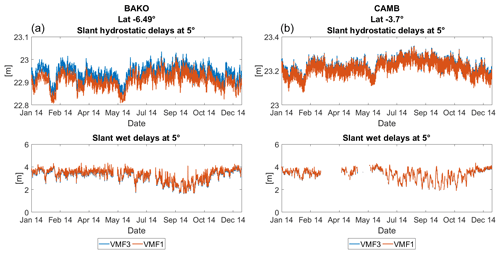
The comparison of slant delays from VMF3 and VMF1 are depicted in Fig. 9. Biases can be seen for the ΔLh at sites BAKO and several other sites. These biases seem to correlate with the bias from GMF, suggesting that the biases come from VMF3.
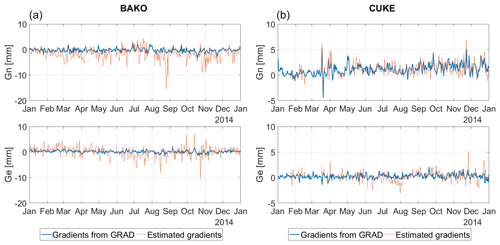
The estimated gradients as obtained from the analysis of GNSS observations are compared with the gradients from the model GRAD. Comparison at two sites, BAKO and CUKE can be seen in Fig. 10. The estimated gradients have larger magnitude compared to gradients from GRAD.
The correlation coefficients for Gn and Ge at site BAKO are 0.41 and 0.33, respectively. The values are similar for the other sites, with the values Gn tending to be larger than Ge. The largest value for Gn is 0.65 at site CUKE, while the largest Ge value is 0.41 at site CNAB, both are located in Papua.
Low correlation coefficients mean that the estimated gradients do not fit well with the gradients from GRAD. The estimated gradients are noisier, possibly because GRAD was determined using NWMs, which are already smoothed. During GNSS data processing, other parameters were also estimated and this might introduce some errors in the results. Gradients are also sensitive to the processing settings, such as the elevation cutoff angle, gradient mapping function, and GNSS constellation, as shown by Kačmařík et al. (2019).
While there are no significant improvements in latitude and longitude, applying VMF3 together with its hydrostatic zenith delays can improve the height component compared to GMF/GPT, as seen from the repeatability. However, in comparison with VMF1, only a slight improvement in the height component can be seen.
Biases at some sites can be seen in the slant hydrostatic delays at 5∘ between VMF3 and both VMF1 and GMF. The estimated gradients are noisier compared to the gradients from the model GRAD, possibly due to the fact that GRAD was determined using smoothed NWMs and errors are introduced during the GNSS processing which can affect the estimated gradient parameters.
It is recommended to use NWM-based mapping functions, such as VMF3 and VMF1. However, considering that the performance of VMF3 is comparable to VMF1, at this point we cannot conclusively recommend using VMF3 in place of VMF1 for GNSS stations in Indonesia.
VMF1 and VMF3 can be downloaded from https://vmf.geo.tuwien.ac.at/trop_products/ (Böhm, 2020).
RINEX data from InaCORS stations can be requested directly from the Indonesian Geospatial Information Agency (BIG).
NP as a first and corresponding author carried out the computation in Bernese. Research idea was first discussed by NP and JB. DL and JB supervised the study and reviewed the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Geodesy Division Sessions G1.1, G2.4, G2.6, G3.1, G4.4, and G5.2”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
The authors would like to thank the Austrian Science Fund (FWF) for supporting this work within project ORD 68-VO. Nabila Putri would like to thank the OeAD for supporting this study through the Ernst Mach-Grants – ASEA-UNINET. The InaCORS data were kindly provided by the Center for Geodetic Control Network and Geodynamics, Indonesian Geospatial Information Agency (PJKGG, BIG).
This research was supported by the FWF Der Wissenschaftsfonds (RADIATE ORD (ORD 68 Open Research Data)), and the OeAD through the Ernst March-Grants – ASEA-UNINET.
This paper was edited by Rosa Pacione and reviewed by two anonymous referees.
Askne, J. and Nordius, H.: Estimation of tropospheric delay for microwaves from surface weather data, Radio Sci., 22, 379–386, 1987. a
Böhm, J.: Index of /trop_products, available at: https://vmf.geo.tuwien.ac.at/trop_products/, last access: 4 March 2020. a
Böhm, J., Niell, A., Tregoning, P., and Schuh, H.: Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data, Geophys. Res. Lett., 33, L07304, https://doi.org/10.1029/2005GL025546, 2006a. a
Böhm, J., Werl, B., and Schuh, H.: Troposphere mapping functions for GPS and VLBI from ECMWF operational analysis data, J. Geophys. Res, 111, B02406, https://doi.org/10.1029/2005JB003629, 2006b. a
Böhm, J., Heinkelmann, R., and Schuh, H.: Short note: a global model of pressure and temperature for geodetic applications, J. Geodesy, 81, 679–683, 2007. a, b
Chen, G. and Herring, T.: Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data, J. Geophys. Res.-Sol. Ea., 102, 20489–20502, 1997. a
Dach, R., Lutz, S., Walser, P., and Fridez, P. (Eds.): Bernese GNSS Software Version 5.2. User manual, Astronomical Institute, University of Bern, Bern Open Publishing, 2015. a
Dach, R., Schaer, S., Arnold, D., Orliac, E., Prange, L., Susnik, A., Villiger, A., and Jäggi, A.: CODE final product series for the IGS, available at: http://ftp.aiub.unibe.ch/CODE/ (last access: 4 March 2020), 2016. a
Kačmařík, M., Douša, J., Zus, F., Václavovic, P., Balidakis, K., Dick, G., and Wickert, J.: Sensitivity of GNSS tropospheric gradients to processing options, Ann. Geophys., 37, 429–446, https://doi.org/10.5194/angeo-37-429-2019, 2019. a
Landskron, D. and Böhm, J.: VMF3/GPT3: refined discrete and empirical troposphere mapping functions, J. Geodesy, 92, 349–360, 2017. a
Landskron, D. and Böhm, J.: Refined discrete and empirical horizontal gradients in VLBI analysis, J. Geodesy, 92, 1387–1399, https://doi.org/10.1007/s00190-018-1127-1, 2018. a
Saastamoinen, J.: Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. In: Henriksen SW et al. (eds) The use of artificial satellites for geodesy, vol 15. AGU, Washington, 247–251, 1972. a