Future TRFs and GGOS – where to put the next SLR station?
Mathis Bloßfeld
Peter König
Florian Seitz
Satellite Laser Ranging (SLR) is one of the four geodetic space techniques contributing to the realisation of terrestrial reference frames (TRFs) as well as to the determination of Earth Rotation Parameters (ERPs). The current SLR tracking network suffers from an insufficient network geometry due to a lack of stations especially in the southern hemisphere. Previous simulation studies have shown that the extension of the global SLR tracking network is indispensable for reaching the target accuracy of future TRFs according to user requests and the ambitious goals of the Global Geodetic Observing System (GGOS). The simulation study presented here puts the focus on a determination of the locations where additional SLR stations are most valuable for an improved estimation of the geodetic parameters.
Within the present study, we perform a simulation of a set of stations distributed homogeneously over the globe and compare different solutions, always adding one of these simulated stations to the real SLR station network. This approach has been chosen in order to be able to investigate the deficiencies of the existing SLR network and to judge in which regions on the globe an additional SLR station would be most valuable for the improvement of certain geodetic parameters of SLR-derived reference frames. It is shown that the optimum location of a future SLR station depends on the parameter of interest. In case of the ERPs, the main potential for improvement by a single additional station can be shown for locations in polar regions (improvement for ypole up to 7 %) and for locations along the equator for the lengh of day (LOD, improvement up to 1.5 %). The TRF parameters would benefit from an additional station around the pierce points of the axes of the terrestrial reference frame (improvement for ty up to 4 %), the Arctic and the Pacific Ocean region (tz improved by up to 4.5 %), and the Antarctic and the Indian Ocean region (scale improved by up to 2.2 %). As outcome of this study, it is concluded that an additional SLR site in the Antarctic region might be of first priority, enabling improvements in the pole coordinates and the scale of the TRF; potential further sites are recommended in the equatorial region, especially beneficial for the origin of the realised TRF as well as for LOD.
Satellite Laser Ranging (SLR) is an important geodetic space technique contributing to the determination of terrestrial reference frames (TRFs), Earth Rotation Parameters (ERPs) as well as coefficients of the Earth’s gravitational field model. SLR is the unique technique allowing us to determine the origin of the reference frame with high accuracy. Moreover, SLR contributes to the determination of the scale. The coordination of the global SLR activities and the distribution of the SLR observations are performed by the International Laser Ranging Service (ILRS; Pearlman et al., 2002). The current SLR ground segment suffers from a non-homogeneous distribution of stations over the globe, especially with a lack of stations in the southern hemisphere, and a permanently changing network geometry due to operating conditions or outages of stations that has an impact on the solved parameters; an effect that is also referred to as the network effect of SLR (Collilieux et al., 2009).
Building new SLR stations carries financial risks and is not only a geographical and technological but also a political decision. Free of these constraints, this simulation study aims at giving a hint for valuable locations of future SLR stations. Within the framework of the Global Geodetic Observing System (GGOS), accuracies of 1 mm for the realised datum parameters and 0.1 mm yr−1 for their rates (Gross et al., 2009) have been defined as requirements. These GGOS requirements recently gained even more importance in view of the United Nations (UN) General Assembly resolution on “A Global Geodetic Reference Frame for Sustainable Development”1.
Due to the importance of the issue, several simulation studies have been performed, putting the focus on various aspects. Several groups performed simulation studies on the effect of a changing SLR network geometry and changing SLR tracking scenarios. Whereas Pavlis and Kuzmicz-Cieslak (2009) compared different scenarios for a possible future SLR network comprising a different number of stations, Kehm et al. (2017) put the focus on the impact of a number of SLR sites which are already under construction or under consideration. Otsubo et al. (2016) performed investigations for a grid of stations distributed equally over the globe. The group from Deutsches GeoForschungsZentrum Potsdam (GFZ) and Technische Universität Berlin performed simulation studies on TRFs estimated via inter-technique combination, simulating observations also for techniques other than SLR, cf., e.g., Glaser et al. (2017), combining simulated SLR and VLBI observations, or Glaser et al. (2019a), combining SLR, VLBI and GPS, also dealing with the issue of the co-location sites (i.e., the datum transfer between the techniques via measured local ties).
A very recent simulation study by Glaser et al. (2019b) performed a comparison of (a) various SLR-only multi-year TRF solutions and (b) various multi-technique multi-year TRF solutions combined from SLR, VLBI and GNSS data. Herein, the SLR network simulated on the basis of a two-satellite setup (LAGEOS-1 and -2) has been modified by (1) adding additional 14 stations on a one-by-one basis to the existing network as well as (2) adding all 14 stations together.
Furthermore, simulation studies putting focus on the impact of an increase of the performances of single stations in the existing network on the estimated TRF parameters and ERPs have been performed, e.g. by Kehm et al. (2018). Beyond the SLR network geometry and station performances, also further SLR-specific aspects that are of importance for the TRF realisation have been subject of simulation studies: Pavlis et al. (2018) presented simulations on the impact of the overall SLR ground-/space segment geometry on the solution, including the tracking of additional targets like GNSS satellites. Andritsch et al. (2017) investigated the impact of different tracking scenarios, putting a special focus on the SLR tracking of GNSS satellites. Bruni et al. (2018) simulated improvements in the SLR network and tracking performance to GNSS satellites, using space ties in order to test the current datum realisation via local ties.
The goal of the study presented hereafter is to determine the regions where stations added to the existing network can bring the largest benefit for the accuracy of the estimated datum parameters and ERPs based on the example of an SLR-derived weekly epoch reference frame (ERF), i.e., a series of weekly solutions for a TRF containing station positions once per week (in contrast to a multi-year reference frame like the ITRF, comprising, in general, station positions at a reference epoch and additionally their velocities; for a comparison between multi-year TRF and ERF realisations cf., e.g., Bloßfeld, 2014; Bloßfeld et al., 2014) and daily estimated sets of ERPs. The simulation study has been performed as a contribution to the GGOS Standing Committee on Performance Simulations and Architectural Trade-offs (GGOS-PLATO) performing a number of activities in order to support the goals of GGOS (Männel et al., 2018).
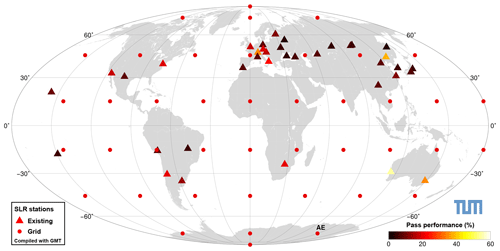
Figure 1Global SLR network and locations of simulated SLR stations. Colours indicate the simulated performance; for existing stations, these were taken from Kehm et al. (2017), for each additional station, a performance of 20 % has been assumed. For the explicit values please refer to Table 2. The station marked with “AE” (Antarctica East) is the station for which an additional scenario with lower performance has been simulated.
We investigate 42 assumed sites, equal-area distributed on a grid around the globe, including both poles. Finally, 43 different solutions are calculated, one comprising the present network only (triangles in Fig. 1), and 42 with the real network plus one additional station (dots in Fig. 1) each. The solutions are calculated on a weekly basis for a time span of five years between 30 December 2012 and 6 January 2018. The general workflow and the error modelling are described in Sect. 2.1, the assumptions for the station-specific performances, i.e., the assumed amount of observations each station produces, are outlined in Sect. 2.2.
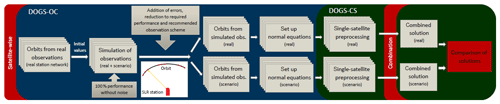
Figure 2Processing chain of the data simulation and solution calculation with DOGS (DGFI Orbit and Geodetic Parameter Estimation Software) -OC (Orbit Computation library) and -CS (Combination and Solution library).
2.1 Workflow and error modelling
Figure 2 shows a schematic view of the processing chain. The computations are performed with the “DGFI Orbit and Geodetic Parameter Estimation Software” (DOGS) developed at DGFI-TUM (Gerstl, 1997; Gerstl et al., 2008). The weekly solutions are combined from a five-satellite setup consisting of Etalon-1/2, LAGEOS-1/2 and LARES.
The simulation and the error modelling were implemented according to the procedure developed by Kehm et al. (2017). In a first step, observations are simulated to orbits estimated from real observations assuming 100 % performance (every theoretically visible pass is observed) for existing as well as for additional stations. Afterwards, the simulated observations are reduced to a station-specific performance determined empirically (for the existing stations, the values are based on approximately 14 months of observation data; taken from the above-mentioned publication) or to an assumed performance of 20 % (for each additional station, as defined as the “goal performance” in the above-mentioned publication; for more details on the chosen performances, please refer to Sect. 2.2). Subsequently, the simulated observations are processed on a weekly basis. In a first step improved initial values for the orbial elements are estimated which are then used for setting up the satellite-specific normal equations (NEQs). The satellite-specific NEQs are subsequently stacked to a common weekly NEQ and finally inverted for the solution. For a detailed description of the workflow please refer to Kehm et al. (2017).
In accordance with Kehm et al. (2017), the functional model for the SLR range measurement ρ is realised as
with rsat being the 3-D satellite position, rsta being the 3-D station position, tM being the approximated epoch of measurement, i.e., reflexion of the laser pulse at the satellite, δt being the time bias of the measurement (here assumed as zero), all modelled systematic effects such as relativistic effects or station-dependent corrections contained in esyst,modelled, and the remaining measurement error ϵ:
Within our simulation, unmodelled systematic effects esyst,unmodelled are represented by variation of the underlying gravity field (EIGEN6S → GGM05S) and ocean tide/loading (EOT11a → FES2004) models, resulting in an orbit RMS of about 3 mm in the case of LARES and below 1 mm in the case of the high orbiting satellites. The behaviour of remaining effects eerr is assumed as white noise with σerr=1 cm, comprising the normal point precision (≤1 mm) as well as all other unmodelled remaining errors. This value has been chosen empirically and is close to the usual maximum of the orbit RMS of <1 cm obtained in our standard SLR processing for a weekly arc.
2.2 Assumptions for the network performance
In this study, the performance of a station is defined as the ratio between the number of passes it could theoretically observe (satellite elevation ; external conditions like the weather not taken into account) w.r.t. the number of passes it actually observed. Table 2 gives an overview of the station-specific performance values applied within this study. All existing stations are set to their empirically derived performance (3 % … 54 % with an average of 13 %, values taken from Kehm et al., 2017). Note: these values were determined for each station in the existing SLR network for a time span between January 2014 and February 2015 which is not identical to the time span of this simulation. However, the performances have been determined excluding longer periods of inactivity ≥1 week and are thus assumed to be representative for each station also in the time span of this simulation study. In the present study, a station in the existing network has been simulated from the point of time on when it started to be active, e.g. Brazilia joining the network from mid-2014 on. Temporary or permanent outages after this point of time have not been taken into account. As to be expected in the near future, the new Argentine-German Geodetic Observatory (AGGO) has been assumed to be operational during the whole time span and has been assigned a performance close to the average of the existing network (15 %).
For each of the other simulated additional stations (i.e., each of the equal-area distributed sites), a common performance of 20 % has been assigned. This common value has been chosen on purpose: We are assuming further improvement of the systems in the foreseeable future; i.e., automated stations equipped with, e.g., kilohertz lasers, fast-slewing telescopes, improved daytime tracking, being able to exploit a much larger amount of the (sometimes short) phases where a satellite is trackable. This would presumably also increase the number of measured passes during predominantly bad weather conditions. Our assumption stands in contrast to simulations using station performances derived from the basis of a total cloud coverage (TCC), as performed in several publications mentioned in the Introduction. As, e.g., pointed out by Glaser et al. (2019b), the TCC alone is not the only aspect that has an effect on the performance of a station and would – neglecting all other performance-relevant aspects – allow for a performance higher than 20 % for all of the existing stations (cf. ibid., Fig. 3).
Free of these imponderables, we thus decided to assign a common performance value of 20 % to each of the additional stations. This could be defined as our “minimum performance goal” for modern laser systems. With a latitude-dependent minimum of 4 and 5 passes per week on the LARES and LAGEOS satellites, resp., each of the assumed sites would fulfil the ILRS Pass Performance Standard2 defining a fixed minimum number of 3500 observed passes per year on all satellites, among them 600 passes on the LAGEOS-class (LAGEOS-1, LAGEOS-2, LARES) satellites (i.e., 4 passes per week on each LAGEOS-class satellite). The aim of the present study is to define potential sites for additional stations given the precondition of comparable conditions at each of these sites.
Within this section, we are going to investigate the impact of a single additional station on the estimated ERPs, i.e., pole coordinates (xpole, ypole) and length-of-day (LOD), as well as on the estimated datum parameters, i.e., Helmert translations (tx, ty, tz), and scale w.r.t. an a priori TRF. As the rotations have been constrained via a No-Net-Rotation condition, they are not analysed in this comparison. The improvement is given in terms of the weighted root mean square (WRMS) of the estimated daily (in case of the ERPs) or weekly (in case of the datum parameters) solutions w.r.t. the a priori values, i.e., it describes how well the a priori values can be retrieved by processing the simulated observations of the stations contained in the simulation scenario. In case of the ERPs, the comparison has been performed w.r.t. the IERS 14 C04 time series (Bizouard et al., 2018). The Helmert parameters have been calculated w.r.t. the SLRF20143, performing a Helmert transformation over all sites of the existing SLR network only (i.e., we determine the indirect effect of an additional station on the estimated datum parameters).
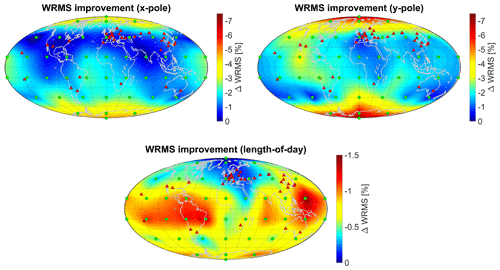
Figure 3Improvement (reduction) of the WRMS of the estimated ERPs by one additional station (note the different scales; for visualisation a triangulation-based natural neighbour interpolation was applied between the grid points).
3.1 Impact of an additional station on the estimated Earth rotation parameters
Figure 3 shows the results for the improvement of the estimated ERPs. It can be clearly seen that the impact of an additional station is systematically affected by the geographical dependence of the sensitivity to a certain ERP which is related to the axes along which the pole coordinates are defined. The maximum improvements for the pole coordinates could be achieved with stations in the polar regions (improvements up to 4.5 % and 7 % for xpole and ypole, respectively) as well as in equatorial regions along the planes through 30∘ W and 180∘ longitude for xpole (defined in the direction of the zero meridian) and through 90∘ E and 90∘ W for ypole (defined in the direction of 90∘ W) with a maximum of about 3 % for both pole coordinates. LOD is predominantly improved by stations in the equatorial region (maximum effect of Earth's rotation), but to a smaller extent by up to 1.5 % (note the different scaling of the colour bars in Fig. 3). It is clearly visible that the potential for improvement is largest for ypole with up to 7 % WRMS improvement, as the xpole plane is already covered by a large number of stations in Europe (close to 0∘ longitude). This is also the reason why the improvement in the plane of 0∘ longitude is reduced and shifted towards the West into the Atlantic ocean, the “gap” between the European/African and American sub-networks. LOD is already well determined due to a distribution of the existing SLR stations in West-East direction. In general, an additional station in the southern hemisphere has a larger potential to improve the estimated ERPs. Moreover, especially sites in the polar regions could help to improve the pole coordinates.
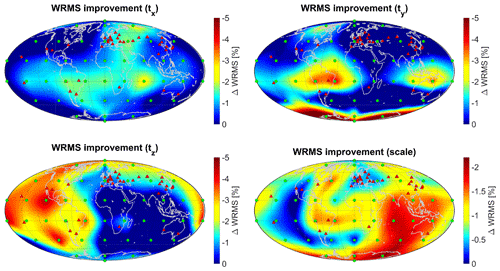
3.2 Impact of an additional station on the estimated parameters of the terrestrial reference frame
Figure 4 shows the geographical dependence of the impact of an additional SLR station on the estimated datum parameters. The results follow a less systematic pattern than the ones obtained for the ERPs. Whereas the potential for improvement of the x-translation tx is a WRMS reduction of up to 2.5 %, larger improvements can be achieved for the y-translation ty by additional sites in the northern part of South America and the northern parts of the Australian continent (WRMS reduced by up to 4 %), as well as in Antarctica (WRMS reduction ≥5 %–7 %). The z-translation tz is mainly improved by stations in the Pacific Ocean region, America, and around the Arctic (WRMS reduction up to 4.5 %). The WRMS of the scale can be improved significantly by up to 2.2 % by stations in America, the Indian Ocean, Australia and Antarctica, as well as to a smaller extent (WRMS reduction up to 1.5 %) by sites in Canada, the Pacific Ocean and the northern part of South America. The rough pattern of these results coincides with the results obtained by Otsubo et al. (2016), especially the large impact of additional stations in Antarctica on ty and in South America on all three translations as well as the generally lower potential of improvement for the scale.
3.3 Special case Antarctica: impact of a lower performance on the results
As could be demonstrated within the previous sections, an additional SLR site in the Antarctic region should be one of the priorities in further investigation on SLR network extensions. However, due to the exterior conditions like a rather high cloud coverage and snow and ice particles transported by katabatic winds, the actual tracking capability of an SLR site at these locations might be lower than the 20 % station performance assumed here. In order to be able to give a measure for the impact of worse tracking conditions on our results, we performed an additional simulation for the grid point located at 75∘ S, 120∘ E, in an area located between the existing Syowa and McMurdo sites already being equipped with VLBI. We assigned a performance of 7 % (half of the average performance of the existing network) and re-performed the analysis for this grid point. With on average 3 passes per week on LAGEOS-1 and LARES and 2 passes per week on LAGEOS-2, this station would perform below the ILRS Pass Performance Standard.
As to be expected, the resulting improvements of the WRMS of the weekly solutions w.r.t. the a priori parameters get smaller. For the datum parameters, this is significantly visible for the y-translation ty where the improvement decreases from 6.4 % to 2.3 %, i.e., by a factor of 2.8. The x- and z- translations and the scale are not largely affected as their improvements have already been rather small for this station. In case of the ERPs, the improvements decrease by a factor of 3.3 on average (cf. Table 1). Thus, if a single station is added to the network but achieves only about one third of the performance we aim at, a significant reduction in the WRMS improvement will be seen; however, the improvements of about 2.3 % (ty) and 1.5 % (pole coordinates) by one single station are still significant, keeping in mind that the maximum values that can be obtained by adding a single station with 20 % performance are at a level of 2 %–7 % for the TRF-defining parameters and as well as for the pole coordinates. This is due to the large improvement of the network and observation geometry by an SLR site in such a location.
Table 1WRMS improvement [%] for the Earth Rotation Parameters for site “AE” with assumed performances of 20 % and 7 %.
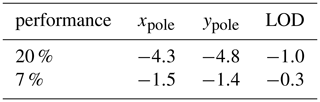
Table 2Simulated pass performances for the stations in the existing network (assumed to include AGGO La Plata) and the additional sites.
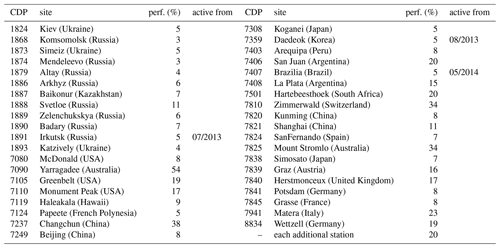
Note: La Plata (Argentina) has been assigned a performance of 15 % which is close to the average of the existing network. All other performances are taken from Kehm et al. (2017) and have been determined empirically for a time span of approximately 14 months. Stations with an empty “active from” column have been assumed to be operational throughout the whole time span from December 2012 to January 2018.
3.4 Interpretation of the results with respect to other simulation approaches
As it has already been outlined in the introduction, we are now in the situation to have various simulation studies from various groups published, each group working with a different approach. The question that arises now is: How do we compare the results?
The simulation studies putting focus on the SLR network evolution are very different in their approaches and not always the full setup and all simulation conditions are clear. For the sake of comparability, we take three of the studies published so far – the present publication, the study by Otsubo et al. (2016), and the study by Glaser et al. (2019b) – and have a look at the different approaches. We are going to limit ourselves to the TRF-defining parameters of an SLR-only TRF as these are common to all of the studies.
The present study is based on a 5-satellite setup comprising a constellation of two high-Earth-orbiting (HEO), two medium-Earth-orbiting (MEO) and one low-Earth-orbiting satellite (LEO) satellite: Etalon-1/2, LAGEOS-1/2 and LARES. We simulate observations which are subsequently processed satellite-wise and then combine the NEQ systems in order to calculate a weekly ERF. Our criterion of interest is the difference of the weekly ERF solutions w.r.t. the a priori TRF, i.e., the WRMS of the weekly Helmert parameters of the solution w.r.t. the a priori TRF. Thus, we are aiming at giving a measure for the repeatability of the solution, i.e., how well can the a priori TRF that has been used as input for the simulation run be re-realised from the simulated observations under the assumed number of active stations (i.e., network geometry), their assumed performance (i.e., the amount and distribution of observations over time), and the assumed observation errors. In contrast to this, the study by Otsubo et al. (2016) uses a 6-satellite setup of two medium-Earth-orbiting (MEO) and four low-Earth-orbiting (LEO) satellites (LAGEOS-1/2, LARES, Ajisai, Stella, Starlette), observed by all stations with a common pass performance of 25 %. Here, no actual parameters are estimated, only the change of the covariance matrices, i.e. the formal errors of the estimated TRF-defining parameters, are used as the criterion of interest. Glaser et al. (2019b) simulate a two-satellite constellation comprising the two LAGEOS satellites. Here, the parameters of interest are the estimated standard deviations of a multi-year TRF estimated for a time span of seven years, determined by processing the simulated observations.
In general, we can state that the different simulation studies lead to a common conclusion, independent from the chosen setup. Stations in the southern hemisphere are crucial to improve the parameters of interest. Otsubo et al. (2016) determine large improvements of up to 17 % in the formal errors of the translations for a site in the Antarctic region, mainly demonstrating the geometrical benefit of such a station, the dense MEO/LEO constellation with different inclinations potentially increasing this geometrical impact compared to the other studies (on the impact of the chosen constellation on the estimated parameters please refer to, e.g. Bloßfeld et al., 2018). The present study confirms the potential of a site in the Antarctic region: For our site “AE”, we could show that the impact of this site may reach up to 5 % reduction in WRMS of the translations if the station performs with a pass performance of 20 %. Assuming a performance of only 7 %, we can still achieve a reduction of 1.5 % which is quite well in accordance with the improvement of about 2 % reduction in the estimated standard deviations of the parameters of a multi-year TRF realised by Glaser et al. (2019b) for the Antarctic site of Syowa (assuming a higher performance of 12 % for this site).
The results shown above indicate that the optimum location for a future SLR station depends on the parameter of interest. In general, we can conclude that for a reliable estimation of ERPs, a systematic distribution of SLR stations in regions around the pierce points of the TRF axes – around which the rotations resembled by the ERPs are defined – is most valuable. The largest potential for the pole coordinates could be found for sites in near-polar regions. For an improved estimation of all ERPs, additional stations within equatorial regions (especially around the longitudes 30∘ W, 180∘, 90∘ W, 90∘ E, where there are gaps in the existing network; the maximum impact of an additional site to be expected around the 0∘ plane is shifted to the West due to the large number of existing stations in Europe) should be considered, as these areas are valuable especially for the pole coordinates but also for LOD. Especially for the realisation of geocentric TRFs, network extensions around the Indian Ocean, Southeast Asia, as well as the Pacific Ocean should be performed. This shows us that, in general, for a reliable datum realisation, a global filling of the gaps in the network has to be recommended in order to obtain an as homogeneously as possible distributed global SLR network. This should be performed especially taking into account possible additional co-location sites, an aspect not treated within this study.
As AGGO has been assumed as permanently operating whereas the other South American stations have been simulated only when actually available, the results also indicate the importance of a permanent 4-site SLR network in South America for the global TRF. The permanent presence of the stations in the northern part of South America with a high performance (Arequipa, Brazilia) proves to be crucial for a reliable estimation of datum parameters and ERPs. In the case of Arequipa it has to be pointed out that the station was performing significantly lower than average within the reference time span; thus, it is recommended to assess if the performance of this site can be increased. In the case of Brazilia, we have to point out that this station has only been available from mid-2014 on and thus has been omitted over a large part of the time span treated within this study (cf. Sect. 2 for the simulation setup). Thus, the new site at Brazilia already fills one of the gaps we found within the present study. To be more general, it has to be pointed out that, of course, not always a set-up of an additional SLR station is necessary. Possibilities to increase the performance of existing stations within the areas determined as valuable for an “additional” station within this study should be examinated. Several rather isolated stations like, especially, Monument Peak (17 % performance and thus close to our “goal performance”) are right in between the simulated additional grid points. As the improvements are determined for fictious sites at these grid points only, the applied interpolation for the sake of visualisation can lead to the impression of larger improvements for some parameters at some of the existing sites. However, we did not choose a denser grid of additional stations due to computing time, as the primary goal if this study is to identify regions of interest for additional sites.
To conclude, as an extension of the network in near-polar regions (e.g. the future site at Ny-Ålesund, cf. Pearlman and Noll, 2018) proves to be valuable for both ERP and TRF, a first priority should be to establish a new site in the Antarctic region as well (e.g. at an existing VLBI site as being investigated for the Japanese site Syowa, cf. Ayoama et al., 2017). As we have shown, a site in Antarctica can still lead to a significant improvement of the estimated parameters even if it performs with a much lower performance than 20 %, its highly positive impact on the network geometry compensating for a potentially reduced performance. Furthermore, additional stations along the equator should be considered. For a number of existing stations, especially along the equatorial region, also a performance enhancement could be an option (cf. Kehm et al., 2017 for the impact of the network performance).
The present study put the focus on SLR-only derived epoch reference frames. We could show that an extension of the existing SLR network is crucial in order to support the ambitious goals of GGOS. However, for the sake of comparability, each additional station has been simulated assuming a common performance of 20 %, a value we assumed to be achievable by the automated systems of the future, given that the weather conditions at the site allow for a sufficient amount of observations. This can be supported by equipping the sites with high-performance kilohertz laser systems allowing to exploit the phases of good weather in order to measure a larger amount of passes. When talking about a new SLR site in a remote area like Antarctica, with a high geometrical impact on the rest of the network, a closer investigation of the so-called Blue-Sky effect, the systematic station displacement due to SLR observing only under good weather conditions, is recommended. Sośnica et al. (2013) determined values for several stations, reaching up to 4.4 mm.
As outlined within the previous sections, our simulation study aimed at a determination of locations that have the potential to improve the estimated TRF parameters and ERPs, assuming comparable conditions for each of these sites, under the assumption of an SLR-only ERF. The locations proposed within this study are therefore intended to indicate where the establishment of additional sites in the SLR network should be investigated with priority. However, if a precise location for a new SLR site is to be defined, a special investigation of this location, taking into account existing SLR stations nearby (e.g.: is a performance enhancement possible?), the actual weather conditions as well as further advantageous features like possible co-locations with other techniques (with measured local ties for the datum transfer), have all to be taken into account as additional factors for a sustainable decision. Beside the TRF datum parameters and ERPs, also the impact of additional sites and improved station performances on the precise orbit determination might be a subject of future investigation.
The observations of the global SLR network used as basis for this study are provided by the International Laser Ranging Service (ILRS) and have been downloaded via the EUROLAS Data Centre (EDC, ftp://edc.dgfi.tum.de/pub/slr/data/npt_crd/; cf. Noll et al., 2018). The simulated observations generated and processed within the framework of this study are no official product and thus not publicly available. They can be provided on request by the corresponding author.
The simulation approach and the chosen scenarios have been developed by AK. MB contributed to the development of the simulation approach as well as to the interpretation of the results. The implementation of the routines, the investigation and the analysis of the results have been performed by AK and PK. FS supervised and coordinated the work within the project. All authors contributed to the final manuscript.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Geodesy Division Sessions G1.1, G2.4, G2.6, G3.1, G4.4, and G5.2”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
This work has been performed within the framework of the project DIrect GEocentric Realisation of the American reference frame by combination of geodetic observation TechnIques (DIGERATI).
This research has been supported by the German Research Foundation (DFG, grant no. SE 1916/5-1).
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
This paper was edited by Johannes Boehm and reviewed by two anonymous referees.
Andritsch, F., Grahsl, A., Dach, R., and Jäggi, A.: Comparing tracking scenarios to LAGEOS and Etalon by simulating realistic SLR observations. Geophysical Research Abstracts, Vol. 19, EGU2017-16642, available at: http://www.bernese.unibe.ch/publist/2017/post/poster_fa.pdf (last access: 30 October 2019), 2017. a
Aoyama, Y., Doi, K., Fukuda, Y., Ikeda, H., Hayakawa, H., Fukuzaki, Y., Sekido, M., Otsubo, T., Nogi, Y., and Shibuya, K.: Geodetic activities at Syowa Station, East Antarctica. Presented at IAG-IASPEI Joint Scientific Assembly, Kobe, Japan, available at: https://confit.atlas.jp/guide/event/iagiaspei2017/subject/G07-4-02/advanced (last access: 19 September 2019), 2017. a
Bizouard, C., Lambert, S., Gattano, C., Becker, O., and Richard, J.-Y.: The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014, J. Geodesy, 93, 621–633, https://doi.org/10.1007/s00190-018-1186-3, 2018. a
Bloßfeld, M.: The key role of Satellite Laser Ranging towards the integrated estimation of geometry, rotation and gravitational field of the Earth, PhD thesis, Reihe C der Deutschen Geodätischen Kommission, ISBN 978-3-7696-5157-7, 2014. a
Bloßfeld, M., Seitz, M., and Angermann, D.: Non-linear station motions in epoch and multi-year reference frames, J. Geodesy, 88, 45–63, https://doi.org/10.1007/s00190-013-0668-6, 2014. a
Bloßfeld, M., Rudenko, S., Kehm, A., Panafidina, N., Müller, H., Angermann, D., Hugentobler, U., and Seitz, M.: Consistent estimation of geodetic parameters from SLR satellite constellation measurements, J. Geodesy, 92, 1003–1021, https://doi.org/10.1007/s00190-018-1166-7, 2018. a
Bruni, S., Rebischung, P., Zerbini, S., Altamimi, Z., Errico, M., and Efisio, S.: Assessment of the possible contribution of space ties on-board GNSS satellites to the terrestrial reference frame, J. Geodesy, 92, 383–399, https://doi.org/10.1007/s00190-017-1069-z, 2018. a
Collilieux, X., Altamimi, Z., Ray, J., van Dam, T., and Wu, X.: Effect of the satellite laser ranging network distribution on geocenter motion estimates, J. Geophys. Res., 114, B04402, https://doi.org/10.1029/2008JB005727, 2009. a
Gerstl, M.: Parameterschätzung in DOGS-OC, DGFI Interner Bericht, MG/01/1996/DGFI, 2nd edn., 1997 (in German). a
Gerstl, M., Müller, H., and Ehrensperger, W.: DOGS-CS. Kombination und Lösung großer Gleichungssysteme, DGFI Interner Bericht, MG/01/1995/DGFI, 2008 (in German). a
Glaser, S., König, R., Ampatzidis, D., Nilsson, T., Heinkelmann, R., Flechtner, F., and Schuh, H.: A Global Terrestrial Reference Frame from simulated VLBI and SLR data in view of GGOS, J. Geodesy, 91, 723–733, https://doi.org/10.1007/s00190-017-1021-2, 2017. a
Glaser, S., König, R., Neumayer, K. H., Nilsson, T., Heinkelmann, R., Flechtner, F., and Schuh, H.: On the impact of local ties on the datum realization of global terrestrial reference frames, J. Geodesy, 93, 655–667, https://doi.org/10.1007/s00190-018-1189-0, 2019a. a
Glaser, S., König, R., Noumayer, K. H., Balidakis, K., and Schuh, H.: Future SLR station networks in the framework of multi-technique terrestrial reference frames, J. Geodesy, online first, https://doi.org/10.1007/s00190-019-01256-8, 2019b. a, b, c, d, e
Gross, R., Beutler, G., and Plag, H.-P.: Integrated scientific and societal user requirements and functional specifications for the GGOS, in: Global Geodetic Observing System, edited by: Plag, H.-P. and Pearlman, M. R., Springer, Berlin Heidelberg New York, 209–224, https://doi.org/10.1007/978-3-642-02687-4_7, 2009. a
Kehm, A., Bloßfeld, M., Pavlis, E. C., and Seitz, F.: Future global SLR network evolution and its impact on the terrestrial reference frame, J. Geodesy, 92, 625–635, https://doi.org/10.1007/s00190-017-1083-1, 2017. a, b, c, d, e, f, g, h
Kehm, A., Bloßfeld, M., and Seitz, F.: Optimization of the current SLR tracking network: potential for SLR-derived reference frames, 21st International Workshop on Laser Ranging, Canberra, Australia, Summary in the proceedings to the 21st IWLR, available at: https://cddis.nasa.gov/lw21/docs/2018/papers/Session4_Kehm_paper.pdf (last access: 21 September 2019), 2018. a
Männel, B., Thaller, D., Rothacher, M., Böhm, J., Müller, J., Glaser, S., Dach, R., Biancale, R., Bloßfeld, M., Kehm, A., Herrera Pinzón, I., Hofmann, F., Andritsch, F., Coulot, D., and Pollet, A.: Recent Activities of the GGOS Standing Committee on Performance Simulations and Architectural Trade-Offs (PLATO), in: International Symposium on Advancing Geodesy in a Changing World, edited by: Freymueller, J. T. and Sánchez, L., International Association of Geodesy Symposia, 149, 161–164, Springer, Cham, https://doi.org/10.1007/1345_2018_30, 2018. a
Noll, C. E., Ricklefs, R., Horvath, J., Mueller, H., Schwatke, C., and Torrence, M.: Information resources supporting scientific research for the international laser ranging service, J. Geodesy, online first, https://doi.org/10.1007/s00190-018-1207-2, 2018. a
Otsubo, T., Matsuo, K., Aoyama, Y., Yamamoto, K., Hobiger, T., Kubo-oka, T., and Sekido, M.: Effective expansion of satellite laser ranging network to improve global geodetic parameters, Earth Planets Space, 68, 65, https://doi.org/10.1186/s40623-016-0447-8, 2016. a, b, c, d, e
Pavlis, E. C. and Kuzmicz-Cieslak, M.: SLR and the Next Generation Global Geodetic Networks, in: Proceedings of the 16th International Laser Workshop, 183–189, edited by: Schillack, S., Space Research Center, Polish Academy of Sciences, Warszawa, Poland, available at: https://cddis.nasa.gov/lw16 (last access: 19 September 2019), 2009. a
Pavlis, E. C., Kuzmicz-Cieslak, M., and Evans, K.: Expanded SLR Target Constellation for Improved Future ITRFs, 21st International Workshop on Laser Ranging, Canberra, Australia, available at: https://cddis.nasa.gov/lw21/docs/2018/posters/A4_Pavlis_Poster.pdf (last access: 19 September 2019), 2018. a
Pearlman, M. R. and Noll, C.: ILRS Central Bureau Report, ILRS Governing Board Meeting with in the framework of the 21st International Workshop on Laser Ranging, Canberra, Australia, available at: https://cddis.nasa.gov/lw21/docs/2018/presentations/ilrsgb_presentations_20181104.pdf (last access: 19 September 2019), 2018. a
Pearlman, M. R., Degnan, J. J., and Bosworth J. M.: The International Laser Ranging Service, Adv. Space Res., 30, 135–143, https://doi.org/10.1016/S0273-1177(02)00277-6, 2002. a
Sośnica, K., Thaller, D., Dach, R., Jäggi, A., and Beutler, G.: Impact of loading displacements on SLR-derived parameters and the consistendy between GNSS and SLR results, J. Geodesy, 87, 751–769, https://doi.org/10.1007/s00190-013-0644-1, 2013. a
UN General Assembly resolution 69/266, available at: https://www.undocs.org/A/RES/69/266 (last access: 14 October 2019)
ILRS Pass Performance Standard, Revision 2015, available at: https://ilrs.cddis.eosdis.nasa.gov/docs/2015/ILRS_passperfstandard_201511.pdf (last access: 14 October 2019)
ftp://cddis.nasa.gov/slr/products/resource/SLRF2014_POS+VEL_2030.0_171024.snx (last access: 30 October 2019)