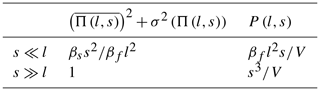On the Density Variability of Poissonian Discrete Fracture Networks, with application to power-law fracture size distributions
Philippe Davy
Caroline Darcel
Romain Le Goc
This paper presents analytical solutions to estimate at any scale the fracture density variability associated to stochastic Discrete Fracture Networks. These analytical solutions are based upon the assumption that each fracture in the network is an independent event. Analytical solutions are developed for any kind of fracture density indicators. Those analytical solutions are verified by numerical computing of the fracture density variability in three-dimensional stochastic Discrete Fracture Network (DFN) models following various orientation and size distributions, including the heavy-tailed power-law fracture size distribution. We show that this variability is dependent on the fracture size distribution and the measurement scale, but not on the orientation distribution. We also show that for networks following power-law size distribution, the scaling of the three-dimensional fracture density variability clearly depends on the power-law exponent.
Characterizing fracture networks in geosciences is a key challenge for many industrial projects such as deep waste disposal, hydrogeology or petroleum resources, because it may change the mechanical (Davy et al., 2018; Grechka and Kachanov, 2006) and hydrological (Bogdanov et al., 2007; De Dreuzy et al., 2001a, b) behaviour of the rock mass. Fractures being ubiquitous and at all scales, the description of these physical properties is often far beyond the reach of a continuum approach (Jing, 2003). Discrete Fracture Networks are computational models explicitly representing the geometry of fractures in a network, and can be used as a basis for physical simulations (mechanical strength, flow, transport…) (see Jing, 2003; Lei et al., 2017, for a review). Considering the scarce nature of geological data, statistical methods have been widely used to generate DFN models, where all fracture geometrical attributes are treated as independent variables from probability distribution derived from the field. Indeed, fracture networks are often described from size distribution, sets of orientations, location, and densities (Dershowitz and Einstein, 1988). Unfortunately, the difficulty of access and resolution to volumetric data makes it difficult to directly measure three-dimensional fracture densities. Stereological analysis proposes theoretical relationship to calculate the 3-D density from 1-D or 2-D measurements under some assumptions (Berkowitz and Adler, 1998; Darcel et al., 2003a; Warburton, 1980). For example, the total fracture surface per unit volume p32 can be calculated from one-dimensional fracture intersections along scanlines or boreholes using some conversion factor (Mauldon, 1994; Terzaghi, 1965; Wang, 2005). Most of these studies focus on characterizing the mean density of a fractured system with poor interest to the underlying variability. However, fracture density variability is an indicator for fracture clustering, which may have dramatical impact on connectivity (Darcel et al., 2003b; La Pointe, 1988; Manzocchi, 2002). Darcel et al. (2013) proposed an analytical solution to quantify at any scale, the standard deviation associated to fracture frequency p10, considering fracture-borehole crossing as a one-dimensional Poisson point process (random positions with fixed density). They show that the standard deviation associated to the number of intersections per unit length p10 is inversely proportional to the square root of the measurement scale. This solution was also demonstrated by Lu et al. (2017), who validated it numerically computing p10 values on boreholes crossing three-dimensional Poissonian DFN models of fixed fracture density. In this paper, we aim to develop analytical solutions for three-dimensional Poissonian DFN models to quantify the range of variability of any kind of fracture density, of any dimension. Particularly, we propose solutions for three-dimensional density variability that cannot be obtained directly from the field. We show that this variability depends on the measurement scale and the fracture size distribution, but not on the orientation distribution. These solutions are validated by numerical simulations, computing the associated fracture densities mean and variance at various scales for three-dimensional Poissonian Discrete Fracture Networks.
In the following, we will calculate the variability of the fracture densities pDd such as defined by Dershowitz and Herda (1992) and Mauldon and Dershowitz (2000). D and d refers to the dimensions of the embedding system Σ and of the fracture trace in Σ, respectively, so that d≤D. For instance, p10 is the number of intersection points (d=0) along a line (D=1) per unit line size. We denote by μf the contribution of a fracture f to pDd (μf is a d-dimension measure) and s the scale at which pDd and μf are calculated so that:
First, we calculate the spatial variability of the measure μf(s) calculated in a D-sphere of size s embedded in a larger space Σ of volume V. In D-dimension, a fracture is represented by an object of dimension D−1 (a point in a scanline, a line in a 2-D outcrop, or a surface in the 3-D space) with a size Sf. The proportion of the total volume occupied by the fracture – i.e., the volume where the measure μf(s) is not nil – is:
We then assume that, when it is not nil, the measure μf(s) derives from a distribution with a mean and a standard deviation . For the total system, we can calculate the first and second order moment of μf(s):
The variance σ2(μf) is written as:
We now sum the contribution of all fractures to calculate . With the Poisson's hypothesis, all fractures are independent events and the variance σ2(μ) is the sum of the variance of each fracture:
And finally, the variability of the density measure pDd is . In the following, we compute the dimensionless ratio between the variance σ2(pDd) and the square of the mean :
In the fractal theory, λ(⋅) is called lacunarity (Plotnick et al., 1996). This is a scale dependent measure, whose analysis gives an idea of the scaling of fracture network textural heterogeneity and potentially on different regimes (Plotnick et al., 1996; Roy et al., 2014).
For geological environments, fracture networks are characterized by a wide distribution of fracture sizes. We denote by n(l) the density distribution of fracture sizes, and n(l)dl is the number of fractures of size in the range per system volume (Davy, 1993). The total number of fractures in a system of volume V is . We then assume that the measure μf(s) and the occupied volume ratio Pf(s) only depends on the fracture size l so that and . Equation (6) can now be written as a function of the fracture size distribution:
In the following, we especially focus on the power-law size distribution, which have been found to adequately fit natural systems (Bonnet et al., 2001; Bour, 2002; Bour and Davy, 1999; Odling, 1997):
with a the power-law exponent, α the density term.
2.1 1-D measurements
Fracture abundance is often quantified on boreholes using the one-dimensional fracture frequency p10 measurement, defined as the number N of crossing fractures per unit borehole length L. If a fracture intersecting this borehole is also part of a subsample of size s, the associated measure . The ratio of subsamples intersected by this fracture is . Considering that s≪L, then , and the lacunarity of such measurement is the one of a one-dimensional Poisson point process (Darcel et al., 2013; Lu et al., 2017):
2.2 3-D measurements
In three-dimensional systems, the fractures d-measures μf are either their occurrence (d=0), surface (d=2) or surrounded sphere (d=3). μf(s) such as defined in the previous section is the part of the measure μf that is included into a domain S of size s, that is the product of μf by the occurrence probability of the fracture to be included into the domain S, Πf,s (also noted Π(l,s) following the notation of the previous section). We define Πf,s as the ratio between the fracture surface included into the domain S to the total fracture surface. If the fracture size is larger than s, both the average value of Πf,s and its standard deviation are proportional to the surface s2. If , that is for large systems, Eqs. (4) and (7) requires to know the expression of . The scaling of and P(l,s) are given in Table 1, with βs and βf shape factors depending on domain S and fractures geometries respectively. This binary model will allow us to simplify the analytical solutions, although we may have significant errors when l∼s.
2.2.1 Fracture number density p30
The p30 measure counts the number of fractures N per unit volume V. Fracture occurrence can be measured as . The corresponding lacunarity under our hypothesis is then given by:
If we consider that fractures have all the same size lf, then:
If we consider now that the network follows a power-law size distribution with minimum and maximum fracture size lmin and lmax, the p30 lacunarity equation is defined by three regimes:
2.2.2 Fracture intensity p32
Fracture intensity p32 measures the total fracture surface per unit volume. The contribution of each fracture of size l in the domain S is . The corresponding lacunarity is then given by:
Following the same reasoning as for p30 density, if we consider that all fractures have the same size lf, we find that the p32 lacunarity follows Eq. (11). If we consider now that the network follows a power-law size distribution, the p32 lacunarity equation is defined by three regimes:
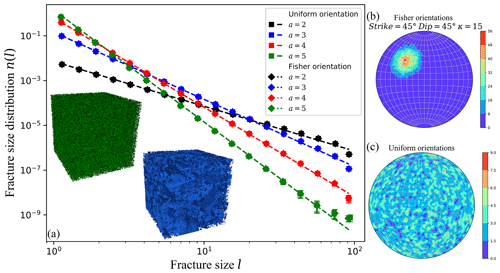
Figure 1(a) Fracture size distribution of generated networks sets (3–6) following power-law size distribution with a bulk density and different power-law exponent a indicated in the legend box (a=3 in blue, a=5 in green), and (b)–(c) stereonets for the two defined orientation distributions.
2.2.3 Percolation parameter p
The percolation parameter gives an idea of the connectivity of the network (Bour and Davy, 1997, 1998; Robinson, 1983). Fundamentally, it is total excluded volume around fractures per unit volume so that for disk-shaped fractures the associated measure (De Dreuzy et al., 2000). The corresponding lacunarity λp is then given by:
If we consider that all fractures have the same size lf, then:
If fracture size distribution follows a power-law size distribution, the percolation parameter lacunarity becomes:
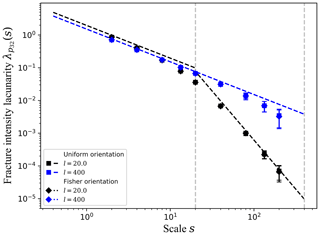
Figure 3Fracture intensity lacunarity curves for networks with constant fracture size and bulk density .
In this section, we aim at validating the analytical solutions developed in Sect. 2, with numerical experiments on Discrete Fracture Networks (DFN). We generate some very simple Poissonian DFN models where the position of each fracture is set randomly within a cubic system of size L=400, and other fracture parameters (orientations, size…) are picked up in the corresponding distribution independently of each other. The fracture shapes are disks, and the diameters l are either constant or power-law distributed. In order to minimize finite-size effects, fracture centers are generated in a cubic box system of size with lmax the largest fracture. We here define two fracture network sets with constant size: (1) and (2) . We also define four fracture network sets (3, 4, 5, 6) following power-law size distribution with , , and where the power-law exponent a is within the range [2,5]. All network sets are simulated for different fracture intensities . We test two different fracture orientation distributions: (a) uniform, all orientations are equally represented, (b) Fisher distribution f(θ,κ) (Fisher, 1953) with a mean pole θ defined by a strike and dip angle both of 45∘, and a dispersion factor κ=15. For statistical analysis, we perform 50 realizations of each fracture sets. Figure 1 shows examples of generated networks and their associated size distributions.
3.1 1-D measurements
We compute the p10 lacunarity curves on 81 boreholes crossing the whole domain, equally spaced and parallel to the z direction, divided in subsamples of size with no overlap. The general p10 lacunarity curve of the system is obtained by stacking the contribution of each borehole. Figure 2 shows that the lacunarity curves associated to the generated Poissonian DFN models with power-law size distribution and mean density follow Eq. (9) as predicted by Darcel et al. (2013) and Lu et al. (2017). When s∼L, the lacunarity curve drops down because of finite-size effects. Lacunarity curves are not the same for the uniform and the Fisher orientation distributions, because the densities are not the same. Indeed, for the same p32 density, the p10 value measured on a borehole depends of the relative orientation between fractures and the borehole. For uniform orientation , and for the defined Fisher orientation p10=0.75p32 which can be found from Wang (2005) formulae.
3.2 3-D measurements
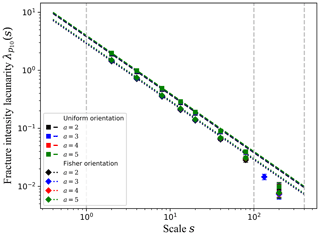
To construct the experimental three-dimensional density lacunarity curves, we divide the cubic domain of size L in L3∕s3 subdomains with no overlap at different scales s. On each subdomain, the three-dimensional fracture densities defined in Sect. 2.2 (p30, p32, p) are computed numerically in order to obtain the associated mean and standard deviation over the whole domain at scale s, giving access to the corresponding lacunarities. For the analytical analysis, we consider that the fracture disk shape factor is , and that the subdomain shape factor is βs=1. Figure 3 focuses on the p32 lacunarity of constant size fracture networks with total fracture intensity . For the case where the fracture size lf=20, Eq. (10) shows two asymptotes for the experimental lacunarity curves for s≪lf and for s≫lf, respectively. When s∼lf, the equations overpredict the lacunarity by a factor of at most 3.
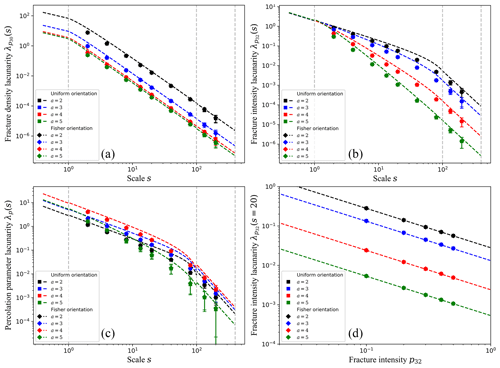
Figure 4 focuses on various 3-D density lacunarity curves for networks following power-law size distributions. When the study scale s is larger than the minimum fracture size lmin, the p30 lacunarity curves (Fig. 4a) evolves as a three-dimensional binomial process (), which is coherent with the fact that fractures are positioned randomly in space. The fracture intensity lacunarity and percolation parameter lacunarity λp (Fig. 4b and c respectively), are divided in three different regimes. When we investigate the dependence upon the scale , their scaling clearly depends of the power-law size distribution exponent a. For large a values (a≥5), the p32 lacunarity curve scales as because small fractures are dominant. For this range of study scale, we can notice a slight discrepancy between the analytical solutions and the numerical experiments. The lower a the larger this discrepancy. This can be explained by the fact that for low a values, the number of fractures whose size l∼s is always significant. Nevertheless, these analytical solutions reproduce well the observed scaling of fracture densities lacunarity. At scale , the difference of p32 lacunarity between networks following either a power-law size distribution of exponent a=2 or a=5 vary up to a factor 103. Finally, Fig. 4d analyses at fixed scale s=20 for different bulk values, highlighting that fracture density lacunarity is inversely proportional to the total fracture density. Finally, for any fracture density, all lacunarity curves are identical whatever the fracture orientation distribution (uniform or Fisher), which proves the orientation independency.
We propose here analytical solutions to quantify the density variability associated to Poissonian fracture networks, using the dimensionless variance parameter λ that we call lacunarity. Solutions are demonstrated for any kind of fracture density of any dimension, with application to uniform and power-law size distribution. The application to other fracture size distribution (exponential, log-normal…) is straightforward. These analytical solutions were validated numerically by computing the density variability on Poissonian DFN models for different bulk density values, fracture size and orientation distributions. We show that the variability of three-dimensional densities is dependent on the study scale and the fracture size distribution, but not on the orientation distribution. Moreover, we show that for networks following power-law size distributions, the scaling of the variability of the fracture intensity p32 is strongly dependent of this power-law exponent. This suggest that the variability of p32 density cannot be estimated from borehole p10 measurements, as it is done to quantify the mean p32 density over the whole network using simple stereological rules. These solutions, which are developed for purely stochastic networks, can thus be used as a reference to estimate three-dimensional fracture density variability on the field, which is out of reach of our investigation technics. Further work is ongoing to quantify the fracture density variability for networks showing fractal correlations (Darcel et al., 2003b), which may also be quantified from the field. We expect the clustering effect associated to such networks to increase significantly the variability of fracture densities and its scaling.
The Python script used for generation and analysis of Discrete Fracture Networks in this paper can be found at https://github.com/elavoine/DFNDensityVariability (last access: 30 May 2019).
EL, PD and CD conceived the idea of this study. EL and PD developed the analytical solutions. EL and RLG developed the code for generation and analysis of DFNs. EL took the lead in writing manuscript, all authors providing critical feedback.
The authors declare that they have no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Division Energy, Resources & Environment (ERE)”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
The authors acknowledge Svensk Kärnbränslehantering AB, the Swedish Nuclear Fuel and Waste Management Company for the funding of this work.
This paper was edited by Thomas Nagel and reviewed by two anonymous referees.
Berkowitz, B. and Adler, P. M.: Stereological analysis of fracture network structure in geological formations, J. Geophys. Res.-Sol. Ea., 103, 15339–15360, https://doi.org/10.1029/98jb01072, 1998.
Bogdanov, I. I., Mourzenko, V. V., Thovert, J. F., and Adler, P. M.: Effective permeability of fractured porous media with power-law distribution of fracture sizes, Phys. Rev. E, 76, 036309, https://doi.org/10.1103/PhysRevE.76.036309, 2007.
Bonnet, E., Bour, O., Odling, N. E., Davy, P., Main, I., Cowie, P., and Berkowitz, B.: Scaling of fracture systems in geological media, Rev. Geophys., 39, 347–383, https://doi.org/10.1029/1999rg000074, 2001.
Bour, O.: A statistical scaling model for fracture network geometry, with validation on a multiscale mapping of a joint network (Hornelen Basin, Norway), J. Geophys. Res., 107, ETG 4-1–ETG 4-12, https://doi.org/10.1029/2001jb000176, 2002.
Bour, O. and Davy, P.: Connectivity of random fault networks following a power law fault length distribution, Water Resour. Res., 33, 1567–1583, https://doi.org/10.1029/96wr00433, 1997.
Bour, O. and Davy, P.: On the connectivity of three-dimensional fault networks, Water Resour. Res., 34, 2611–2622, https://doi.org/10.1029/98wr01861, 1998.
Bour, O. and Davy, P.: Clustering and size distributions of fault patterns: Theory and measurements, Geophys. Res. Lett., 26, 2001–2004, https://doi.org/10.1029/1999gl900419, 1999.
Darcel, C., Bour, O., and Davy, P.: Stereological analysis of fractal fracture networks, J. Geophys. Res.-Sol. Ea., 108, 2451, https://doi.org/10.1029/2002jb002091, 2003a.
Darcel, C., Bour, O., Davy, P., and de Dreuzy, J. R.: Connectivity properties of two-dimensional fracture networks with stochastic fractal correlation, Water Resour. Res., 39, 1272, https://doi.org/10.1029/2002wr001628, 2003b.
Darcel, C., Davy, P., and Le Goc, R.: Development of the statistical fracture domain methodology – application to the Forsmark site, SKB R-13-54, Svensk Kärnbränslehantering AB (SKB), Stockholm, 2013.
Davy, P.: On the frequency-length distribution of the San Andreas fault system, J. Geophys. Res.-Sol. Ea., 98, 12141–12151, 1993.
Davy, P., Darcel, C., Le Goc, R., and Mas Ivars, D.: Elastic Properties of Fractured Rock Masses With Frictional Properties and Power Law Fracture Size Distributions, J. Geophys. Res.-Sol. Ea., 123, 6521–6539, https://doi.org/10.1029/2017jb015329, 2018.
De Dreuzy, J.-R., Davy, P., and Bour, O.: Percolation parameter and percolation-threshold estimates for three-dimensional random ellipses with widely scattered distributions of eccentricity and size, Phys. Rev. E, 62, 5948–5952, https://doi.org/10.1103/PhysRevE.62.5948, 2000.
De Dreuzy, J.-R., Davy, P., and Bour, O.: Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 1. Effective connectivity, Water Resour. Res., 37, 2065–2078, https://doi.org/10.1029/2001wr900011, 2001a.
De Dreuzy, J.-R., Davy, P., and Bour, O.: Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 2. Permeability of networks based on lognormal distribution of apertures, Water Resour. Res., 37, 2079–2095, https://doi.org/10.1029/2001wr900010, 2001b.
Dershowitz, W. S. and Einstein, H. H.: Characterizing rock joint geometry with joint system models, Rock Mech. Rock Eng., 21, 21–51, 1988.
Dershowitz, W. S. and Herda, H. H.: Interpretation of fracture spacing and intensity, The 33th US Symposium on Rock Mechanics (USRMS), American Rock Mechanics Association, Santa Fe, New Mexico, 1992.
Fisher, R. A.: Dispersion on a sphere, Proc. R. Soc. Lon. Ser.-A, 217, 295–305, 1953.
Grechka, V. and Kachanov, M.: Effective elasticity of fractured rocks: A snapshot of the work in progress, Geophysics, 71, W45–W58, 2006.
Jing, L.: A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering, Int. J. Rock Mech. Min., 40, 283–353, https://doi.org/10.1016/s1365-1609(03)00013-3, 2003.
La Pointe, P.: A method to characterize fracture density and connectivity through fractal geometry, Int. J. Rock Mech. Min., 25, 421–429, 1988.
Lei, Q., Latham, J.-P., and Tsang, C.-F.: The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks, Comput. Geotech., 85, 151–176, https://doi.org/10.1016/j.compgeo.2016.12.024, 2017.
Lu, Y. C., Tien, Y. M., and Juang, C. H.: Uncertainty of 1-D Fracture Intensity Measurements, J. Geophys. Res.-Sol. Ea., 122, 9344–9358, https://doi.org/10.1002/2016jb013620, 2017.
Manzocchi, T.: The connectivity of two-dimensional networks of spatially correlated fractures, Water Resour. Res., 38, 1-1–1-20, 2002.
Mauldon, M.: Intersection probabilities of impersistent joints, Int. J. Rock Mech. Min., 31, 107–115, 1994.
Mauldon, M. and Dershowitz, W.: A multi-dimensional system of fracture abundance measures, Geological Society of America Abstracts with Programs, 32, p. A474, 2000.
Odling, N. E.: Scaling and connectivity of joint systems in sandstones from western Norway, J. Struct. Geol., 19, 1257–1271, 1997.
Plotnick, R. E., Gardner, R. H., Hargrove, W. W., Prestegaard, K., and Perlmutter, M.: Lacunarity analysis: a general technique for the analysis of spatial patterns, Phys. Rev. E, 53, 5461, https://doi.org/10.1103/PhysRevE.53.5461, 1996.
Robinson, P.: Connectivity of fracture systems-a percolation theory approach, J. Phys. A-Math. Gen., 16, 605, https://doi.org/10.1088/0305-4470/16/3/020, 1983.
Roy, A., Perfect, E., Dunne, W. M., and McKay, L. D.: A technique for revealing scale-dependent patterns in fracture spacing data, J. Geophys. Res.-Sol. Ea., 119, 5979–5986, https://doi.org/10.1002/2013jb010647, 2014.
Terzaghi, R. D.: Sources of error in joint surveys, Geotechnique, 15, 287–304, 1965.
Wang, X.: Stereological interpretation of rock fracture traces on borehole walls and other cylindrical surfaces, PhD Thesis, Virginia Polytechnic Institute and State, Blacksburg, VA, USA, 2005.
Warburton, P.: A stereological interpretation of joint trace data, Int. J. Rock Mech. Min., 17, 181–190, 1980.