Separating physical impacts from natural variability using piggybacking technique
Wojciech W. Grabowski
In a chaotic system, like moist convection, it is difficult to separate the impact of a physical process from effects of natural variability. This is because modifying even a small element of the system physics typically leads to a different system evolution and it is difficult to tell whether the difference comes from the physical impact or it merely represents a different flow realization. This paper discusses a relatively simple and computationally efficient modelling methodology that allows separation of the two. The methodology is referred to as the piggybacking approach. The idea is to use two sets of thermodynamic variables (the temperature, water vapor, and all aerosol, cloud, and precipitation variables) in a single cloud simulation. The two sets differ in a specific element of the physics, such as aerosol properties, microphysics parameterization, large-scale forcing, environmental profiles, etc. One thermodynamic set is coupled to the dynamics and drives the simulated flow, and the other set piggybacks the flow, that is, thermodynamic variables are carried by the flow but they do not affect it. By switching the two sets (i.e. the set driving the simulation becomes the piggybacking one, and vice versa), the impact on the cloud dynamics can be evaluated. This paper provides details of the method and reviews results of its application to such problems as the postulated deep convection invigoration in polluted environments, the impact of changes in environmental profiles (e.g., due to climate change) on convective dynamics, and the role of cloud-layer heterogeneities for shallow convective cloud field evolution. Prospects for applying piggybacking technique to other areas of atmospheric simulation (e.g., weather prediction or geoengineering) are also mentioned.
-
Please read the editorial note first before accessing the article.
-
Article
(454 KB)
-
Please read the editorial note first before accessing the article.
Moist convection is an example of a chaotic system. Typically, a simple modification of its physics results in a different evolution of a cloud or cloud field. For natural clouds, a classical example is the inability to separate effects of a convective cloud seeding from highly unpredictable convective cloud evolution. In a nutshell, it is impossible to tell how the seeded cloud would evolve without seeding, or to what extent the unseeded cloud would change when seeded. One possibility is to study many clouds either seeded or not seeded, and to apply statistical techniques to assess the impact of seeding. For the modelling, the ensemble approach, conceptually similar to observing many seeded and unseeded clouds, can be used. However, one needs to use an appropriate number of ensemble members for a confident separation of the physical impact from the natural variability. The ensemble size can be selected by considering the ensemble spread resulting for the natural variability simulations (i.e., without seeding) and the mean difference between seeded and unseeded ensembles. To be statistically significant, the mean difference between the two ensembles needs to be larger than the ensemble spread (how much larger depends of the selected confidence level). Hence, larger ensembles are needed for more chaotic systems, that is, when the natural variability is large. Here we present a method that is relatively straightforward and computationally more efficient than the ensemble approach and which allows a confident assessment of the physical process impact. We refer to this technique as piggybacking. The next section explains the basic idea of the approach. Section 3 provides a brief review of problems to which the piggybacking has been recently applied. A discussion in Sect. 4 concludes the paper.
Figure 1 illustrates the piggybacking approach. The crux of the approach is to apply two sets of thermodynamic variables (the potential temperature, water vapor mixing ratio, and all variables describing aerosol, cloud, and precipitation particles) in a single simulation. The set 1 is coupled to the dynamics (u, v, and w wind components and pressure p in the figure) and drives the simulation (the driver). The coupling is represented in the figure by the blue lines with arrows at both ends. Thermodynamic variables from the set 2 are advected by the flow and are exposed to the same physical processes as in the set 1 (e.g., surface fluxes, phase changes, precipitation fallout, etc.). However, the set 2 does not affect local buoyancy and thus does not impact the simulated flow. Hence, the set 2 “piggybacks” the flow and it is referred to as the piggybacker. This is marked in the figure by blue lines with arrows pointing from the dynamics to the thermodynamics only. The only difference between the two sets of thermodynamic variables is in the specific element of the model physics that is investigated (e.g., a specific parameter of a microphysical scheme, different aerosol characteristics, the initial sounding, etc.). An important element of the piggybacking approach is switching thermodynamic sets in the second simulation so the driving set becomes the piggybacking set, and vice versa. This is the key difference between the upper and lower panels in Fig. 1. In practical terms, the “switching thermodynamic sets” refers to the way the buoyancy – the only link between thermodynamics and dynamics (at least in the incompressible or anelastic system) – is calculated, that is, applying thermodynamics variables from either the set 1 (the upper panel in Fig. 1) or the set 2 (the lower panel). In a compressible system, the coupling also concerns the impact on the pressure as well as on the air density fields, so the coupling between dynamics and thermodynamics is more involved.
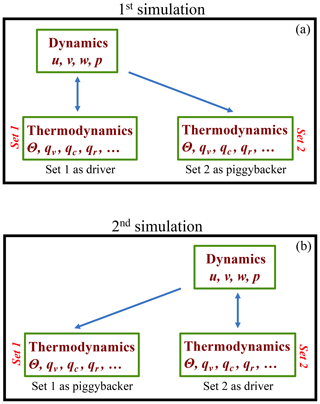
Figure 1The schematic of the piggybacking methodology. (a) shows the first simulation in which set 1 of thermodynamic variables drives the simulation and the set 2 piggybacks the simulated flow. This is reversed in (b), where the second simulation is driven by the set 2 of thermodynamic variables and the set 1 piggybacks the simulated flow. The dynamic variables are the velocity components u, v, w and pressure p. Thermodynamic variables include the potential temperature θ, water vapor mixing ratio qv, all cloud qc, all precipitation qr, and all other variables that thermodynamics needs (e.g., aerosols).
In general, one should expect different flow evolutions between the upper and lower panels of Fig. 1 because of the change in the physics between sets 1 and 2. However, the focus of the analysis is on comparing the driver-piggybacker differences (such as the cloud top height, cloud fraction, surface precipitation, etc.) between the two simulations, and not the difference between the drivers. The former represents the impact of the physics that is investigated (e.g., a parameter in the microphysics scheme) in the specific realization of the flow, whereas the latter includes the impact of that parameter on the flow dynamics. For instance, in the case of the microphysics scheme impact on the surface precipitation, diver-piggybacker difference shows enhancement or reduction of the surface precipitation given the same cloud-scale flow. Hence, the impact of the scheme on the dynamics is eliminated and only the microphysical effect is left. In contrast, comparing surface precipitation from the drivers in the two simulations shown in Fig. 1 involves combination of dynamical effects (e.g., stronger updrafts, deeper clouds, etc.) and microphysical effects (e.g., more efficient conversion of cloud condensate to precipitation). Moreover, driver and piggybacker thermodynamic variables can be compared grid-point by grid-point (for instance, to demonstrate the impact of the microphysical scheme on the buoyancy in conditionally-sampled cloudy volumes) in addition to comparing driver-piggybacker difference for various statistics, such as the mean surface precipitation, mean cloud top height, or mean cloud fraction.
The two piggybacking simulations (i.e., upper and lower panels in Fig. 1) are obviously computationally more expensive than two simulations featuring only single set of thermodynamic variables, that is, as in traditional simulations investigating the impact of a modified physics. However, the alternative is to apply an ensemble of traditional simulations with the number of ensemble members large enough so the impact can be extracted in confidence as explained above. The computational cost of such ensemble simulations would be significantly higher. Below we review applications of the piggybacking methodology and hope the above general comments are well illustrated with specific applications.
The initial applications of the piggybacking approach focused on the cloud microphysics, for instance, comparing cloud field simulations applying different microphysics schemes or different scheme parameters (Grabowski, 2014, 2015; Grabowski and Jarecka, 2015; Grabowski and Morrison, 2016, 2017). Such simulations applied the same initial sounding for both the driver and the piggybacker thermodynamic sets. Grabowski (2014) demonstrated that application of the piggybacking allows confident assessment of the impact of assumed cloud droplet concentration on rainfall from shallow convection. A small ensemble of simulations (5 members) was not sufficient to provide statistically-significant assessment when only differences between drivers were considered. This was because the ensemble-averaged difference between drivers was significantly smaller than the mean ensemble spread. A much larger ensemble would be needed as explained in the introduction. In contrast, comparing drivers and piggybackers for each ensemble member allowed for a statistically significant assessment.
Grabowski (2015) applied piggybacking technique to illustrate the impact of two single-moment bulk microphysics parameterizations (with the differences concerning mostly the ice phase) on simulations of daytime development of deep unorganized convection. Motivated by the suggestion in Rosenfeld et al. (2008), the so-called “convective invigoration in polluted environments”, the study also considered the impact of prescribed cloud droplet concentration on convective dynamics. The key argument in Rosenfeld et al. (2008) is that suppressed warm-rain processes below the freezing level in polluted conditions lead to more liquid water transported in convective drafts through the melting level. This provides additional buoyancy when the liquid water freezes aloft. However, such an argument neglects the negative impact of the liquid condensate on the buoyancy. In fact, it is simple to show that the negative impact of liquid condensate weight and the positive impact of the latent heat released by freezing the condensate almost exactly cancel each other. Thus, the invigoration is only possible when the frozen condensate is “off-loaded” through precipitation processes. The modelling setup developed in Grabowski et al. (2006) was used. Simulations in Grabowski (2015) show that extracting small differences in the surface precipitation, cloud cover, and liquid and ice water paths is possible with unprecedented fidelity using piggybacking. Having two sets of thermodynamic variables allowed grid-point by grid-point comparison of cloud buoyancy between the driver and the piggybacker. Such an analysis clearly demonstrates that the cloud buoyancy above the freezing level is only weakly affected by contrasting cloud droplet concentrations. This casts doubt on the invigoration hypothesis for unorganized deep convection as suggested in Rosenfeld et al. (2008), at least when investigated applying a single-moment bulk microphysics.
Grabowski and Morrison (2016) applied piggybacking with the double-moment bulk warm-rain and ice microphysics of Morrison and Grabowski (2007, 2008a, b) to look at the invigoration hypothesis using more comprehensive microphysics. Important differences from the single moment schemes in Grabowski (2015) were the inclusion of supersaturation prediction (rather than applying the saturation adjustment) and linking the ice initiation to cloud droplet concentration and size (e.g., leading to higher ice concentrations in the polluted case). These two were critical for the simulated impacts. Finite supersaturation below the freezing level, higher in the pristine case, affected the cloud buoyancy and thus cloud updraft strength below the freezing level. As in Grabowski (2015), applying piggybacking allowed exposing grid-point by grid-point buoyancy differences below the freezing level due to different supersaturations in pristine and polluted conditions. Buoyancy differences above the freezing level were small, again in agreement with the approximate balance between the liquid condensate weight and the latent heating due to freezing. However, higher cloud droplet concentrations led to higher ice concentrations and thus to smaller ice crystal sizes, lower sedimentation rates, and thus more extensive anvil coverage in the final couple hours of the simulations. Thus, piggybacking allowed separation of the dynamic effect (more buoyancy below the freezing level due to lower supersaturations in the polluted case) from the microphysical effect related the larger extent of upper-tropospheric anvils. Note that in observations (using satellite data in particular) the larger extent of upper-tropospheric anvils in polluted conditions can be erroneously interpreted as the effect of convection invigoration rather than just the microphysical effect (see discussion in Morrison and Grabowski, 2011).
Piggybacking simulations applying the same setup as in Grabowski (2015) and Grabowski and Morrison (2016) with the University of Pecs bin microphysics scheme (e.g., Geresdi, 1998; Rasmussen et al., 2002; Xue et al., 2010, 2012; Geresdi et al., 2014) included into the NCAR's Weather Research and Forecasting (WRF) model were recently completed (Noemi Sarkadi, U. of Pecs, Hungary; personal communication, 2019). Bin microphysics provides more comprehensive approach to model cloud processes and thus using it to test the invigoration hypothesis applying the same model setup is worthwhile. The results of piggybacking bin simulations are broadly consistent with those of Grabowski and Morrison (2016). They show a small dynamic effect (i.e., insignificant invigoration) and a large microphysical effect. However, specific details (e.g., upper tropospheric cloud fractions) are different between bin and double-moment microphysics simulations. A manuscript describing these results is being drafted.
Grabowski and Jarecka (2015) and Grabowski and Morrison (2017) discuss the impact of condensation modelling (e.g., predicting supersaturation versus saturation adjustment) in shallow and deep convection, respectively, applying the piggybacking methodology. For the nonprecipitating shallow convection, Grabowski and Jarecka (2015) contrast single-moment bulk microphysics applying saturation adjustment with bin microphysics that predicts in-cloud supersaturation. The bin condensation scheme was applied assuming wide range of cloud droplet concentrations, from about 5 to over 4000 cm−3. The results show that the differences in cloud fields simulated with bulk and bin schemes come not from small differences in the condensation, but from more significant differences in the evaporation of cloud water near cloud edges as a result of entrainment and mixing with the environment. Grabowski and Morrison (2017) applied the Grabowski et al. (2006) case of daytime convective development over land applying the double-moment scheme used in Grabowski and Morrison (2016) and focused on the impact of either predicting the in-cloud supersaturation or applying saturation adjustment. Results show a significant impact on deep convection dynamics, with saturation adjustment featuring more cloud buoyancy and thus stronger updrafts. This leads to a noticeable increase of the surface rain accumulation. Upper-tropospheric anvil cloud fractions increase when the supersaturation is predicted because of the increased ice concentrations and thus longer residence times of anvil particles. The increase of ice concentrations is because a few percent water supersaturation in strong updrafts above the freezing levels translates into larger ice supersaturations that impact the ice initiation.
Zachary Lebo (U. of Wyoming) and Graham Feingold (NOAA) applied piggybacking technique to separate dynamical and microphysical impacts of aerosol loading on the simulated precipitation efficiency in various cloud types, from tropical convective clouds to continental convective clouds and marine boundary layer clouds. The simulations applied high-spatial-resolution WRF model with a double-moment bulk microphysics scheme. These results were reported in a presentation entitled ”Microphysical and dynamical factors controlling the precipitation efficiency response to changes in aerosol loading” at the 2016 International Conference on Clouds and Precipitation (ICCP; Exeter, UK; see the abstract S12.6 at http://www.meeting.co.uk/confercare/iccp2016/Oral and Poster Abstracts.pdf, last access: 3 September 2019).
The above studies applied the same initial profiles for both the driver and for the piggybacker, and focused on the differences in the representation of cloud microphysics. Grabowski (2018) applied piggybacking in series of simulations where the two sets of thermodynamic variables differed in the initial sounding (e.g., slightly different temperature or moisture profiles) or different forcing (modified Bowen ratio of the surface flux or prescribed large-scale moisture and temperature tendencies). The motivation was to show that the separation of aerosol impacts (i.e., the hypothesized convection invigoration in polluted environments) from effects of meteorological factors that independently affect moist convection is impossible, at least for the daytime development of unorganized deep convection considered in that study. The key argument is that the accuracy of atmospheric measurements is not sufficient to allow the clear separation of meteorological factors affecting convection from the impact of aerosols. Grabowski and Prein (2019) applied piggybacking to study the impact of climate-change-related modification of temperature and moisture profiles. The piggybacking was applied to separate the dynamic and thermodynamic factors affecting convection. Dynamic factors concern, for instance, different convective available potential energy (CAPE) and convective inhibition (CIN) of the initial sounding. The thermodynamic factor concerns effects of the water vapor increase that the warmer atmosphere can hold and convection can work with. The separation of dynamic and thermodynamic factors is possible through piggybacking because the dynamics affects the difference between the drivers, whereas the thermodynamics affects the driver-piggybacker difference.
Piggybacking was also applied in simulations where one of the thermodynamic sets applied homogenization of the cloud environment to explore whether environmental heterogeneities, such as remnants of previous clouds, affect subsequent cloud developments; Kurowski et al. (2019). The difference between driver and piggybacker was in either including or excluding the homogenization of the cloud environment. It was shown that applying the homogenization had a relatively small impact on the subsequent evolution of the shallow convection cloud field. Recently, piggybacking was used to show that cloud-radiation interactions have a small impact on the evolution of a shallow convection cloud field. This was accomplished by comparing simulations in which radiative transfer scheme was applied either in the column-by-column mode (i.e., emphasizing differences between cloudy and cloud-free columns) or using horizontally-uniform radiative cooling resulting from horizontal averaging of the column-by-column radiative transfer. Small differences between simulations applying horizontally-heterogeneous radiative cooling and its horizontally-averaged profile clearly show that cloud-radiation interactions have a small impact on shallow convection evolution. A manuscript discussing these results is under preparation (Marcin Kurowski, personal communication, 2019).
In summary, the studies briefly described above provide strong support for the benefits of the piggybacking method. The technique seems relatively simple to implement in a numerical model (“embarrassingly simple” as stated in the opening sentence of Sect. 2 of Grabowski, 2014). However, its implementation by others, especially in the WRF community model, faces challenges difficult to overcome.
The piggybacking approach explained in Sect. 2 was previously tried in a simplified form. In studies concerning the impact of microphysical parameterizations on deep organized convection (e.g., squall lines), Jiwen Fan (PNNL) and Zachary Lebo (U. of Wyoming) independently tried to use different microphysics schemes with only one temperature and only one water vapor mixing ratio. In other words, the temperature and water vapor mixing ratio from the set driving the flow were applied to the second set of condensed-water variables (e.g., cloud ice and snow). In such a case, the microphysical tendencies from the piggybacking variables did not affect the temperature and moisture. For instance, the supersaturation derived using the driver temperature and water vapor was applied for the piggybacker variables. As a result, the simplified approach led after some time to unrealistic condensed-phase variables when compared to the driving variables, that is, those that included microphysical feedback on the temperature and water vapor. Similar problems were encountered when applying the simplified methodology in ice scheme comparisons (Axel Seifert, DWD, personal communication, 2019). Such an inconsistency is eliminated when the two sets include the temperature and water vapor as both sets of thermodynamic variables are then thermodynamically consistent.
A common criticism of the piggybacking approach (e.g., Jiwen Fan, personal communication, 2018, 2019) is that the piggybacking thermodynamic variables are inconsistent with the flow predicted by the driver thermodynamics. For instance, the buoyancy that drives the flow is typically different from the buoyancy derived from the piggybacking variables (e.g., Grabowski and Morrison, 2016). This is of course a valid point and nothing can be done to correct that. However, one should consider the following points. First, the piggybacker set can be thought as an analogue of the thermodynamic set applied in the kinematic model simulations (e.g., Szumowski et al., 1998; Morrison and Grabowski, 2007, 2008b; Slawinska et al., 2009). In such a case, the flow is prescribed (e.g., from an analytic formula as in references above), and the fact that thermodynamic variables have nothing to do with the prescribed flow is never discussed. Second and perhaps more important point is that each thermodynamic set has a chance to drive the flow as illustrated in Fig. 1. This is why there are two piggybacking simulations, with each set driving once and then piggybacking once. The two simulations have typically different flow evolutions. For instance, the cloud fields are different after some time for the case of cloud field simulations discussed in Grabowski and Morrison (2016), see Fig. 2 therein. The key point, however, is that the analysis focuses on the driver-piggybacker differences, and not on the differences between the drivers as in the parallel simulations without piggybacking. For this, the fact that the two simulations (i.e., with either set driving) have different flow realization is less important.
Moreover, piggybacking approach as applied in the papers discussed in this review is not to run a single pair of piggybacking simulations, but a small ensemble for each. For instance, Grabowski (2014, 2015) applied a five-member mini-ensembles in simulations of shallow and deep convection cloud fields. Members of the mini-ensemble typically differ in the random number set that is applied at the onset of the simulations and sometimes used during the model run (like in the case of shallow to deep convection transition of Grabowski et al., 2006). Although the ensemble members do feature different flow realizations, the driver-piggybacker differences are often similar for all ensemble members. For instance, the surface rain accumulations in the simulations discussed in Grabowski (2014; Table 1 therein) and in Grabowski and Morrison (2016, cf. Figs. 6 and 13) show some spread among the drivers, but the driver-piggybacker difference is small. Moreover, having a small ensemble allows to compare the spread between the drivers in one ensemble (i.e., the natural variability) to the driver-piggybacker difference between the two ensembles. The ensembles can be small (just a few members suffice) because the analysis focusses on the driver-piggybacker difference and not on the difference between the two drivers. In the latter case, a large number of ensemble members would be needed for a statistically significant estimation of the physical impact as previously discussed.
One can ask a question if it is possible to have the difference between the driver and the piggybacker so large that the physical consistency of the piggybacking set is severely compromised. For instance, can driver and piggybacker form clouds in different places, with the cloud field eventually looking completely different? We do not think this is possible in situations when clouds form as a result of the vertical motion in the atmosphere, as in the case of convection. This has been indirectly shown in Grabowski (2014) where the difference in the instantaneous surface rain rates from shallow convective clouds follow nicely between the driver and piggybacker with a small offset between the two (see Fig. 3 therein). In Grabowski and Jarecka (2015, see Fig. 6 and its discussion), the cloud fraction in shallow convection cloud field simulations vary systematically between bulk and bin microphysics, the latter assuming different aerosol characteristics. As argued in Grabowski and Jarecka (2015), this is consistent with a picture of individual clouds having slightly different widths because of different cloud-edge evaporation in each scheme (i.e., gradual in the bin scheme and instantaneous in the bulk scheme). However, the situation might be different when simulated clouds form due to processes other than vertical motion. For instance, it remains to be seen if the piggybacking technique is appropriate to study clouds that form due to radiative cooling (e.g., radiation fog) or stratiform clouds where both the vertical motion and radiative processes are important.
Finally, sensitivity of simulated convection to the representation of cloud microphysics is well appreciated by the modelling community. At the same time, natural variability of atmospheric flows is at heart of numerical weather prediction (NWP) and the ensemble prediction is the most common technique to account for that. With the advance of convection-permitting NWP (i.e., applying nonhydrostatic models with horizontal grid lengths in the range of 1 to 5 km and with no need for deep convection parameterization), representation of microphysics and the natural variability become closely linked. Although ensemble prediction typically focuses on the forecast sensitivity to the initial conditions, the sensitivity to the microphysics representation needs also to be kept in mind, especially for convective weather situations. Thus, the ensemble may also include members that only differ in the representation of cloud and precipitation physics. Would then including the piggybacking technique for some members be beneficial? We would think so. The way piggybacking can then be used is that some ensemble members provide the input (i.e., the flow) for several thermodynamic sets that result in a range of surface precipitation realizations with the same atmospheric flows. Such approach might turn out beneficial for hydrological applications. One may also consider other elements of the NWP model physics (e.g., radiative transfer, surface fluxes) as worthy candidates to be included into the piggybacking technique as well.
In summary, we believe that piggybacking provides a useful and computationally efficient method to separate the impact of physical processes from the natural variability in simulations of a chaotic system such as atmospheric moist convection.
The used data in this publication were taken from https://doi.org/10.1175/JAS-D-14-0231.1 (Grabowski, 2014), https://doi.org/10.1175/JAS-D-14-0307.1 (Grabowski, 2015), and https://doi.org/10.1175/JAS-D-18-0105.1 (Grabowski, 2018), https://doi.org/10.1175/JAS-D-15-0091.1 (Grabowski and Jarecka, 2015), https://doi.org/10.1175/JAS-D-15-0367.1 (Grabowski and Morrison, 2016), and https://doi.org/10.1175/JAS-D-16-0255.1 (Grabowski and Morrison, 2017), https://doi.org/10.1175/JCLI-D-19-0007.1 (Grabowski and Prein, 2019), and https://doi.org/10.1029/2018GL080847 (Kurowski et al., 2019).
The author declares that there is no conflict of interest.
This article is part of the special issue “European Geosciences Union General Assembly 2019, EGU Division Energy, Resources & Environment (ERE)”. It is a result of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019.
This work was partially supported by the U.S. DOE ASR Grant DE-SC0016476 and by the National Center of Meteorology, Abu Dhabi, UAE, under the UAE Research Program for Rain Enhancement Science (UAE-NATURE project). Any opinions, findings and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Center of Meteorology, Abu Dhabi, UAE. NCAR is sponsored by the National Science Foundation.
This research has been supported by the U.S. Department of Energy (grant no. DE-SC0016476) and the National Center of Meteorology, Abu Dhabi, UAE (UAE-NATURE project).
This paper was edited by Gregor Giebel and reviewed by two anonymous referees.
Geresdi, I.: Idealized simulation of the Colorado hailstorm case: Comparison of bulk and detailed microphysics, Atmos. Res., 45, 237–252, https://doi.org/10.1016/S0169-8095(97)00079-3, 1998.
Geresdi, I., Sarkadi, N., and Thompson, G.: Effect of the accretion by water drops on the melting of snowflakes, Atmos. Res., 149, 96–110, https://doi.org/10.1016/j.atmosres.2014.06.001, 2014.
Grabowski, W. W.: Extracting microphysical impacts in large eddy simulations of shallow convection, J. Atmos. Sci. 71, 4493–4499, https://doi.org/10.1175/JAS-D-14-0231.1, 2014.
Grabowski, W. W.: Untangling microphysical impacts on deep convection applying a novel modeling methodology, J. Atmos. Sci., 72, 2446–2464, https://doi.org/10.1175/JAS-D-14-0307.1, 2015.
Grabowski W. W.: Can the impact of aerosols on deep convection be isolated from meteorological effects in atmospheric observations?, J. Atmos. Sci., 75, 3347–3363, https://doi.org/10.1175/JAS-D-18-0105.1, 2018.
Grabowski, W. W. and Jarecka, D.: Modeling condensation in shallow nonprecipitating Convection, J. Atmos. Sci., 72, 4661–4679, https://doi.org/10.1175/JAS-D-15-0091.1, 2015.
Grabowski, W. W. and Morrison, H.: Untangling microphysical impacts on deep convection applying a novel modeling methodology. Part II: Double-moment microphysics, J. Atmos. Sci., 73, 3749–3770, https://doi.org/10.1175/JAS-D-15-0367.1, 2016.
Grabowski, W. W. and Morrison, H.: Modeling condensation in deep convection. J. Atmos. Sci., 74, 2247–2267, https://doi.org/10.1175/JAS-D-16-0255.1, 2017.
Grabowski, W. W. and Prein, A. F.: Separating dynamic and thermodynamic im- pacts of climate change on daytime convective development over land, J. Climate, 32, 5213–5234, https://doi.org/10.1175/JCLI-D-19-0007.1, 2019.
Grabowski, W. W., Bechtold, P., Cheng, A., Forbes, R., Halliwell, C., Khairoutdinov, M., Lang, S., Nasuno T., Petch, J., Tao, W.-K., Wong, R., Wu, X., and Xu, K.-M.: Daytime convective development over land: a model intercomparison based on LBA observations, Q. J. Roy. Meteorol. Soc., 132, 317–344, https://doi.org/10.1256/qj.04.147, 2006.
Kurowski, M. J., Suselj, K., and Grabowski, W. W.: Is shallow convection sensitive to environmental heterogeneities?, Geophys. Rev. Lett. 46, https://doi.org/10.1029/2018GL080847, 2019.
Morrison, H. and Grabowski, W. W.: Comparison of bulk and bin warm rain microphysics models using a kinematic framework, J. Atmos. Sci., 64, 2839–2861, https://doi.org/10.1175/JAS3980, 2007.
Morrison, H. and Grabowski, W. W.: Modeling supersaturation and subgrid-scale mixing with two-moment bulk warm microphysics, J. Atmos. Sci., 65, 792–812, https://doi.org/10.1175/2007JAS2374.1, 2008a.
Morrison, H. and Grabowski, W. W.: A novel approach for representing ice micro- physics in models: description and tests using a kinematic framework, J. Atmos. Sci., 65, 1528–1548, https://doi.org/10.1175/2007JAS2491.1, 2008b.
Morrison, H. and Grabowski, W. W.: Cloud-system resolving model simulations of aerosol indirect effects on tropical deep convection and its thermodynamic environment, Atmos. Chem. Phys., 11, 10503–10523, https://doi.org/10.5194/acp-11-10503-2011, 2011.
Rasmussen, R. M., Geresdi, I,. Thompson, G., Manning, K., and Karplus, E.: Freezing drizzle formation in stably stratified layer clouds: The role of radiative cooling of cloud droplets, cloud condensation nuclei, and ice initiation., 2002, J. Atmos. Sci., 59, 837–860, https://doi.org/10.1175/1520-0469(2002)059<0837:FDFISS>2.0.CO;2, 2002.
Rosenfeld, D., Lohmann, U., Raga, G. B.,O'Dowd, C. D, Kulmala, M., Fuzzi, S.,Reissell, A., and Andreae, M. O.: Flood or drought: How do aerosols affect precipitation?, Science, 321, 1309–1313, https://doi.org/10.1126/science.1160606, 2008.
Slawinska, J., Grabowski, W. W., and Morrison, H.: Impact of atmospheric aerosols on precipitation from deep organized convection: A prescribed-flow modeling study using double-moment bulk microphysics, Q. J. Roy. Meteorol. Soc., 135, 1906–1913, https://doi.org/10.1002/qj.450, 2009.
Szumowski, M. J., Grabowski, W. W., and Ochs, H. T.: Simple two–dimensional kinematic framework designed to test warm rain microphysical models, Atmos. Res. 45, 299–326, https://doi.org/10.1016/S0169-8095(97)00082-3, 1998.
Xue, L., Teller, A., Rasmussen, R. M., Geresdi, I., and Pan, Z.: Effects of aerosol solubility and regeneration on warm-phase orographic clouds and precipitation simulated by a detailed bin microphysical scheme, J. Atmos. Sci., 67, 3336–3354, https://doi.org/10.1175/2010JAS3511.1, 2010.
Xue, L., Teller, A., Rasmussen, R. M., Geresdi, I., Pan, Z., and Liu, X.: Effects of aerosol solubility and regeneration on mixed-phase orographic clouds and precipitation, J. Atmos. Sci., 69, 1994–2010, https://doi.org/10.1175/JAS-D-11-098.1, 2012.
Please read the editorial note first before accessing the article.
- Article
(454 KB) - Full-text XML





