Evaluation of random forests and Prophet for daily streamflow forecasting
Georgia A. Papacharalampous
Hristos Tyralis
We assess the performance of random forests and Prophet in forecasting daily streamflow up to seven days ahead in a river in the US. Both the assessed forecasting methods use past streamflow observations, while random forests additionally use past precipitation information. For benchmarking purposes we also implement a naïve method based on the previous streamflow observation, as well as a multiple linear regression model utilizing the same information as random forests. Our aim is to illustrate important points about the forecasting methods when implemented for the examined problem. Therefore, the assessment is made in detail at a sufficient number of starting points and for several forecast horizons. The results suggest that random forests perform better in general terms, while Prophet outperforms the naïve method for forecast horizons longer than three days. Finally, random forests forecast the abrupt streamflow fluctuations more satisfactorily than the three other methods.
- Article
(4487 KB) -
Supplement
(616 KB) - BibTeX
- EndNote
Streamflow forecasting is important due to its engineering-oriented implementation in flood and water resources management. The large variety of relevant applications includes flood and drought prediction, irrigation and reservoir operation applications (see, for example, Zhang et al., 2018). Therefore, improved hydrological forecasts in various time scales can benefit the society. Data-driven, including machine learning, models are commonly used for streamflow (or river discharge and reservoir inflow) forecasting. The latter can be performed by exclusively using observed streamflow data, as in Papacharalampous et al. (2017a, 2018a) and Zhang et al. (2018), or by also using information obtained from predictor variables (e.g. precipitation variables). Such examples are available in Jain et al. (2018), and Tyralis and Papacharalampous (2018). Recent studies by Papacharalampous et al. (2017a, b, 2018a, b, c), and Tyralis and Papacharalampous (2017) suggest that several classical and/or popular forecasting algorithms are mostly equally useful for hydrological applications when exploiting information from past observations only. Improvements may result from the use of suitable predictor variables.
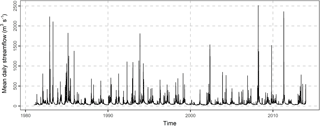
Figure 1Mean daily streamflow of Current river at Doniphan, Missouri (longitude: −90.85, latitude: 36.62) for the years 1981–2013.
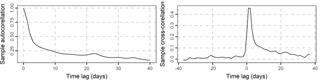
Figure 2Sample autocorrelation of the daily streamflow of the Current river and sample cross-correlation with the daily precipitation of the basin. The sample cross-correlation is the estimate of Corr[xi, yi+j], where Corr is the cross-correlation function.
Let xi and yi denote daily precipitation and mean daily streamflow at day i = 1,…, n. If the observations are known up to day k, then the j-step ahead forecast is defined as the forecast of the random variable yk+j obtained by using information up to day k. Herein, we assess the performance of random forests and Prophet for j-step ahead forecasting. These two models are introduced by Breiman (2001), and Taylor and Letham (2018a) respectively. The former is a popular machine learning technique successfully applied in forecasting competitions. Tyralis and Papacharalampous (2017) optimize its forecasting use when it is exclusively provided with past information for the process to be forecasted, while here additional information for predictor variables is considered. Random forests are also used in data-driven rainfall-runoff applications (e.g. Shortridge et al., 2016; Petty and Dhingra, 2018), which are similar to forecasting applications with the exception that the predictor variables are considered to be known until time k+j and streamflow until time . Moreover, streamflow prediction applications of random forests can be found in Lima et al. (2015) and Papacharalampous et al. (2017a, 2018a, b). Prophet is an automatic time series forecasting model, which also allows the incorporation of predictor variables, as well as the computation of prediction intervals. The latter is proposed, for instance, in Tyralis and Koutsoyiannis (2014). Papacharalampous et al. (2018c) investigate the performance of Prophet in monthly temperature and precipitation forecasting without utilizing predictor variables. This is also the way used herein. Since benchmarking forecasting results is essential, we implement a naïve method and a multiple linear regression model alongside with the above outlined sophisticated ones. Our aim is to illustrate important facts about the models for the problem under examination.
We forecast the mean daily streamflow of Current River at Doniphan, Missouri (see Fig. 1). The daily precipitation data xi at the basin and the mean daily streamflow data yi span in the time period 1981–2013. This dataset was compiled by Addor et al. (2017b, see also the data availability section). The sample autocorrelation Corr[yi, yi+j] and the sample cross-correlation Corr[xi, yi+j] are presented in Fig. 2. The sample autocorrelation is higher than 0.4 for time lag up to three days, while the sample cross-correlation is higher than 0.4 for time lag up to two days. A correlation equal to 0.4 means that the predictor variable can explain approximately 16 % of the variance of the dependent variable in a linear regression model between yi and xi.
Subsequently we present the forecasting methods of this study, while further implementation details can be found in the code availability section. The forecasts of the naïve benchmark at time k+j, j = 1,…, 7 are equal to yk, i.e. they are equal to the last observation. The use of this benchmark is documented in Hyndman and Athanasopoulos (2018, Chap. 3.1). Multiple linear regression models are also widely implemented benchmarks (see Solomatine and Ostfeld, 2008). Herein, they are used for benchmarking the results of random forests; therefore, the predictor variables utilized by these two methods are identical. These predictor variables are reported below together with the justification of their selection. For the same methods, streamflow and precipitation data are pre-processed using the square root, as proposed by Messner (2018), with the aim for them to be normalized.
Prophet is based on the idea of fitting Generalized Additive Models. Its documentation is available in Taylor and Letham (2018a), while details about its software implementation can be found in Taylor and Letham (2018b). We examine three variations of the Prophet model. In the first variation (hereafter named as “Prophet 1”; the remaining variations are named in a similar way) we decompose the streamflow time series up to time k using the STL method (Cleveland et al., 1990) and remove the seasonal component. Then Prophet is fitted to the decomposed time series, it forecasts at times k+j, j = 1,…, 7 and, finally, the seasonal component is added to the forecast. Prophet 2 is fitted to the streamflow time series up to time k, and forecasts at times k+j, j = 1,…, 7. In this variation the seasonal component is automatically handled by Prophet. Prophet 3 uses the last 30 observed values for fitting.
Literature and technical information on the implementation of random forests is available in Verikas et al. (2011), and Biau and Scornet (2016). Random forests are easy to tune and implement due to the low number of parameters (see also Scornet et al., 2015). Their main parameter is the number of trees. Higher number of trees results in predictions that are more accurate; however, in this case the computation time increases substantially, while there is also an asymptotic limit in the accuracy of the model (see, for example, Biau and Scornet, 2016). We use 100 trees, which is considered as a reasonable and balanced choice regarding their accuracy (with respect to the limit of accuracy) and computational cost (Probst and Boulesteix, 2018). The other parameters are set equal to the default values, as in the implementation by Wright (2018). To forecast 1-step ahead (i.e. to forecast yk+1) we use xk−2, xk−1, xk, yk−3, yk−2, yk−1, yk and the month of the yk+1 as predictor variables. We also used a lower number of predictor variables and the performance (not presented here for reasons of brevity) was similar. Using more predictor variables would result in considerably higher computation time with little expected gain in performance. We use the month of yk+1 for considering the seasonality effect. To forecast yk+2 we use again xk−2, xk−1, xk, yk−3, yk−2, yk−1, yk and the month of yk+2 as predictor variables. We apply the same procedure to forecast yk+j, j = 3,…, 7. Regarding the training period, if we want to forecast yk+1, random forests are fitted using the respective xi−3, xi−2, xi−1,yi−4, yi−3, yi−2, yi−1 as predictor variables and yi as dependent variable for i = 1,…, k. Each time that a new forecast is required (i.e. when i increases by 1), the model is trained again, so that it includes the latest information. A similar procedure is followed for longer forecast horizons.
Forecasting is performed for all days in the years 2004–2013. The reason for using 1∕3 of the dataset for testing is justified on the ground of the large variability of streamflow explained from climatic and other factors (e.g. Kingston et al., 2006; Li et al., 2018; Tyralis et al., 2018). Testing in an independent set is also a standard practice in the assessment of data-driven models (e.g. Solomatine and Ostfeld, 2008; Elshorbagy et al., 2010a, b; Wu et al., 2014). In particular for observations up to day k we forecast the streamflow at days k+j, j = 1,…, 7. We produce forecasts for values of k in {2003-12-21,…, 2013-12-30}. The forecasts are summarized conditional upon the forecasting method and the forecast horizon.
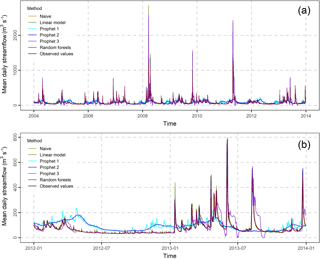
Section 3 is devoted to the presentation of the results, which emphasizes on the 1-, 4- and 7-day ahead forecasts. In Figs. S1 and S2 (see the Supplement) we present these forecasts in comparison to the observations, while Fig. 3 focuses on the 1-day ahead forecasts. The differences between the methods are better presented in Fig. S2 in the Supplement. This figure zooms in the period 2012–2013. In general, the forecasts of the naïve, multiple linear regression and random forests methods are close to their target values. When the length of the forecast horizon increases, the distance between the observations and the forecasts increases as well. The forecasts of Prophet 1 and 2 are smooth lines, i.e. they do not capture the abrupt streamflow changes. In addition, they lay far from the actual streamflow values. The forecasts of Prophet 3 seem to be in better agreement with the observed streamflow; still, they are worse than those produced by the naïve, multiple linear regression and random forests methods.
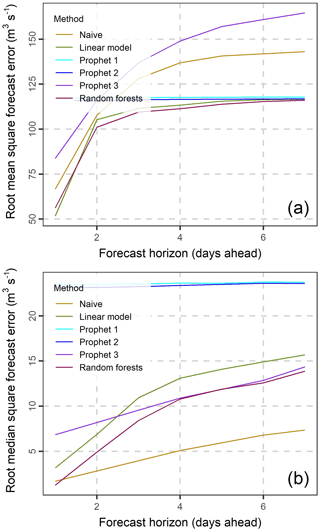
In Fig. 4 we present the root mean square errors (RMSE) and root median square errors (RMdSE) for all forecast horizons. Random forests have the lowest RMSE followed by the multiple linear regression, the naïve and Prophet 3 methods for short forecast horizons (with length less than three days). For forecast horizons longer than four days random forests still perform the best, while Prophet 1 and 2 are better than the naïve and Prophet 3 methods. The performance of the naïve, multiple linear regression and random forests methods decreases with increasing length of the forecast horizon and gets stabilized for long forecast horizons due to the reduction of the available information used by the predictor variables. Prophet 1 and 2, on the other hand, seem to have a constant performance for all forecast horizons. In terms of RMdSE the naïve method is better than Prophet 3, which in turn is better than Prophet 1 and 2 for all forecast horizons. The performance of Prophet 1 and 2 is constant regardless of the forecast horizon. Random forests are the best method for the 1-day ahead forecast horizon, and the second best for the 2-day ahead and higher forecast horizons. RMdSE is lower than RMSE for all methods.
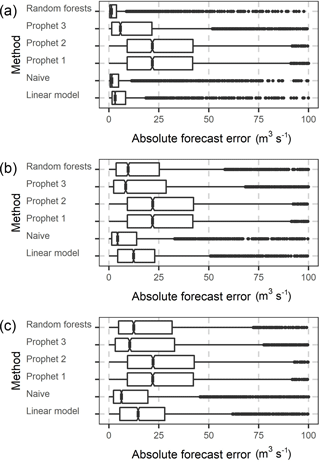
Figure 5Notched boxplots of the absolute forecast errors of the 1, 4 and 7-step ahead forecasts (a to c) of the daily streamflow of Current river in the period 2004–2013. The x axis of the three graphs has been truncated at 100 m3 s−1.
To further investigate the above rankings and the difference in the magnitude between RMSE and RMdSE, in Fig. 5 we present the notched boxplots of the absolute errors for the 1-, 4- and 7-day ahead forecast horizons. The medians of the absolute error are similar to the RMdSE values presented in Fig. 4. The boxplots are positively skewed, resulting in higher RMSE than RMdSE values. In addition, the dispersion of absolute errors is higher for longer forecast horizons.
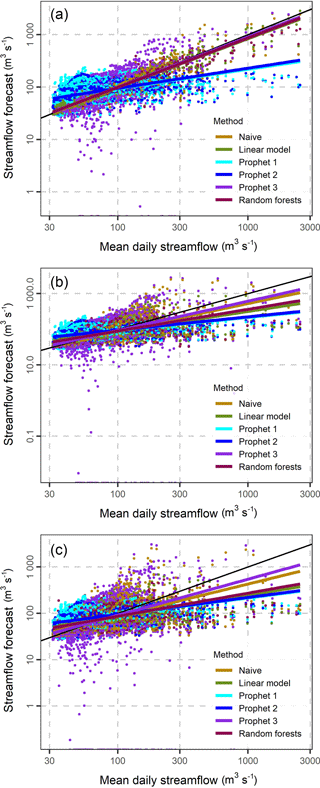
Figure 61-, 4- and 7-step ahead forecasts (a to c) and their corresponding mean daily streamflow values. The black line corresponds to forecasts equal to observations, while the remaining lines are the plots of the linear regression models fitted between forecasts and observations.
To understand how close the forecasts are to their corresponding observations we present the scatterplots of Fig. 6. For all the methods excluding Prophet 1 and 2 the plots of the linear models fitted between the forecasts and the observations are close to the black line, which corresponds to forecasts equal to the observations, indicating a good performance in 1-day ahead forecasting. The distance between the black line and the other linear regression lines increases, when the forecast horizon increases. The increase is less pronounced for the Prophet 1 and 2 methods.
In summary, the following remarks are important, especially in light of Abrahart et al. (2008) who comment on the need for documenting the performance assessment of data-driven models on the grounds of specific questions. Random forests are a better predictor compared to the multiple linear regression models, while they outperform the naïve method in terms of root mean square error. The use of the selected precipitation predictor variables considerably improves the forecasts, probably due to the nature of the examined problem; however, their influence diminishes for forecast horizons longer than four days. This is also expected from the magnitude of autocorrelations and cross-correlations with precipitation, which indicate that precipitation should influence the magnitude of streamflow for some days. The forecasting error of the Prophet 1 and 2 methods (which are fitted to the whole sample) is independent of the forecast horizon. Nevertheless, these two methods perform consistently worse than the other methods in terms of root median square error, while they have a comparable (to the other methods) performance in terms of root mean square error. Furthermore, Prophet exhibits a worse performance than the naïve method when it exclusively uses observations from the last 30 days (Prophet 3). Random forests are a good method for obtaining optimal forecasts, while their performance could be further improved by using more predictor variables, e.g. temperature variables. The naïve method is also good; therefore, it should be used as a benchmark, in spite of the fact that it is rarely met in the hydrological forecasting literature. The Prophet model should be used for forecasting at long horizons.
We note that this study is among the first implementing random forests and Prophet for streamflow forecasting. We have thoroughly investigated the performance of all methods, looking at their predictive performance at several forecast horizons. The visualization of all aspects helped in better understanding important facts about the models' performance and, thus, could be used as a guide for the assessment of methods in streamflow forecasting.
This paper is easily reproducible using the R Programming Language (R Core Team, 2018). We used the following R packages: bestNormalize (Peterson, 2018), devtools (Wickham et al., 2018b), gdata (Warnes et al., 2017), ggplot2 (Wickham, 2016; Wickham et al., 2018a), gridExtra (Auguie, 2017), knitr (Xie, 2014; 2015; 2018), lubridate (Grolemund and Wickham, 2011; Spinu et al., 2018), prophet (Taylor and Letham, 2018b), ranger (Wright, 2018; Wright and Ziegler, 2017), readr (Wickham et al., 2017), rmarkdown (Allaire et al., 2018), scales (Wickham, 2018), stringi (Gagolewski, 2018), zoo (Zeileis and Grothendieck, 2005; Zeileis et al., 2018).
The data used in the present study can be obtained from the CAMELS dataset (Addor et al., 2017a, b; Newman et al., 2014, 2015). The daily precipitation data included in the CAMELS dataset were sourced by Thornton et al. (2014).
The supplement related to this article is available online at: https://doi.org/10.5194/adgeo-45-201-2018-supplement.
The authors declare that they have no conflict of interest.
We thank the Editor Luke Griffiths and one anonymous reviewer, whose comments
have led to the improvement of this paper. Edited by:
Luke Griffiths
Reviewed by: Luke Griffiths and one anonymous
referee
Abrahart, R. J., See, L. M., and Dawson, C. W.: Neural Network Hydroinformatics: Maintaining Scientific Rigour, in: Practical Hydroinformatics, edited by: Abrahart, R. J., See, L. M., and Solomatine, D. P., Springer-Verlag Berlin Heidelberg, 33–47, https://doi.org/10.1007/978-3-540-79881-1_3, 2008.
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: Catchment attributes for large-sample studies, Boulder, CO, UCAR/NCAR, https://doi.org/10.5065/D6G73C3Q, 2017a.
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: The CAMELS data set: catchment attributes and meteorology for large-sample studies, Hydrol. Earth Syst. Sci., 21, 5293–5313, https://doi.org/10.5194/hess-21-5293-2017, 2017b.
Allaire, J. J., Xie, Y., McPherson, J., Luraschi, J., Ushey, K., Atkins, A., Wickham, H., Cheng, J., and Chang, W.: rmarkdown: Dynamic Documents for R. R package version 1.10, available at: https://CRAN.R-project.org/package=rmarkdown (last access: 16 August 2018), 2018.
Auguie, B.: gridExtra: Miscellaneous Functions for “Grid” Graphics, R package version 2.3, available at: https://CRAN.R-project.org/package=gridExtra (last access: 16 August 2018), 2017.
Biau, G. and Scornet, E.: A random forest guided tour, TEST, 25, 197–227, https://doi.org/10.1007/s11749-016-0481-7, 2016.
Breiman, L.: Random Forests, Mach. Learn., 45, 5–32, https://doi.org/10.1023/A:1010933404324, 2001.
Cleveland, R. B., Cleveland, W. S., McRae, J. E., and Terpenning, I.: STL: A Seasonal-Trend Decomposition Procedure Based on Loess, J. Off. Stat., 6, 3–33, 1990.
Elshorbagy, A., Corzo, G., Srinivasulu, S., and Solomatine, D. P.: Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology – Part 1: Concepts and methodology, Hydrol. Earth Syst. Sci., 14, 1931–1941, https://doi.org/10.5194/hess-14-1931-2010, 2010a.
Elshorbagy, A., Corzo, G., Srinivasulu, S., and Solomatine, D. P.: Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology – Part 2: Application, Hydrol. Earth Syst. Sci., 14, 1943–1961, https://doi.org/10.5194/hess-14-1943-2010, 2010b.
Gagolewski, M.: stringi: Character String Processing Facilities, R package version 1.2.4, available at: https://CRAN.R-project.org/package=stringi (last access: 16 August 2018), 2018.
Grolemund, G. and Wickham, H.: Dates and Times Made Easy with lubridate, J. Stat. Softw., 40, https://doi.org/10.18637/jss.v040.i03, 2011.
Hyndman, R. J. and Athanasopoulos, G.: Forecasting: Principles and Practice, available at: https://otexts.org/fpp2/ (last access: 16 August 2018), 2018.
Jain, S. K., Mani, P., Jain, S. K., Prakash, P., Singh, V. P., Tullos, D., Kumar, S., Agarwal, S. P., and Dimri, A. P.: A Brief review of flood forecasting techniques and their applications, Int. J. River Basin Man., https://doi.org/10.1080/15715124.2017.1411920, 2018.
Kingston, D. G., Lawler D. M., and McGregor, G. R.: Linkages between atmospheric circulation, climate and streamflow in the northern North Atlantic: research prospects, Prog. Phys. Geography, 30, 143–174, https://doi.org/10.1191/0309133306pp471ra, 2006.
Li, L., Schmitt, R. W., and Ummenhofe, C. C.: The role of the subtropical North Atlantic water cycle in recent US extreme precipitation events, Clim. Dynam., 50, 1291–1305, https://doi.org/10.1007/s00382-017-3685-y, 2018.
Lima, A. R., Cannon, A. J., and Hsieh, W. W.: Nonlinear regression in environmental sciences using extreme learning machines: A comparative evaluation, Environ. Model. Softw., 73, 175–188, https://doi.org/10.1016/j.envsoft.2015.08.002, 2015.
Messner, J. W.: Chapter 11 – Ensemble Postprocessing With R, in: Statistical Postprocessing of Ensemble Forecasts, edited by: Vannitsem, S., Wilks, D. S., and Messner, J. W., Elsevier, 291–329, https://doi.org/10.1016/B978-0-12-812372-0.00011-X, 2018.
Newman, A. J., Sampson, K., Clark, M. P., Bock, A., Viger, R. J., and Blodgett, D.: A large-sample watershed-scale hydrometeorological dataset for the contiguous USA, Boulder, CO, UCAR/NCAR, https://doi.org/10.5065/D6MW2F4D, 2014.
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Error evolution in multi-step ahead streamflow forecasting for the operation of hydropower reservoirs, Preprints, 2017100129, https://doi.org/10.20944/preprints201710.0129.v1, 2017a.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Forecasting of geophysical processes using stochastic and machine learning algorithms, Eur. Water, 59, 161–168, 2017b.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes, Preprints, 2017100133, https://doi.org/10.20944/preprints201710.0133.v2, 2018a.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: One-step ahead forecasting of geophysical processes within a purely statistical framework, Geosci. Lett., 5, https://doi.org/10.1186/s40562-018-0111-1, 2018b.
Papacharalampous, G., Tyralis, H., and Koutsoyiannis, D.: Predictability of monthly temperature and precipitation using automatic time series forecasting methods, Acta Geophys., 66, 807–831, https://doi.org/10.1007/s11600-018-0120-7, 2018c.
Peterson, R. A.: bestNormalize: Normalizing Transformation Functions, R package version 1.2.0, available at: https://CRAN.R-project.org/package=bestNormalize (last access: 16 August 2018), 2018.
Petty, T. R. and Dhingra, P.: Streamflow Hydrology Estimate Using Machine Learning (SHEM), J. Am. Water Resour. As., 54, 55–68, https://doi.org/10.1111/1752-1688.12555, 2018.
Probst, P. and Boulesteix, A. L.: To tune or not to tune the number of trees in random forest, J. Mach. Learn. Res., 18, 1–18, 2018.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 16 August 2018), 2018.
Scornet, E., Biau, G., and Vert, J. P.: Consistency of random forests, Ann. Stat., 43, 1716–1741, https://doi.org/10.1214/15-AOS1321, 2015.
Shortridge, J. E., Guikema, S. D., and Zaitchik, B. F.: Machine learning methods for empirical streamflow simulation: a comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds, Hydrol. Earth Syst. Sci., 20, 2611–2628, https://doi.org/10.5194/hess-20-2611-2016, 2016.
Solomatine, D. P. and Ostfeld, A.: Data-driven modelling: some past experiences and new approaches, J. Hydroinform., 10, 3–22, https://doi.org/10.2166/hydro.2008.015, 2008.
Spinu, V., Grolemund, G., and Wickham, H.: lubridate: Make Dealing with Dates a Little Easier, R package version 1.7.4, available at: https://CRAN.R-project.org/package=lubridate (last access: 16 August 2018), 2018.
Taylor, S. J. and Letham, B.: Forecasting at scale, Am. Stat., 72, 37–45, https://doi.org/10.1080/00031305.2017.1380080, 2018a.
Taylor, S. J. and Letham, B.: prophet: Automatic Forecasting Procedure, R package version 0.3.0.1, available at: https://CRAN.R-project.org/package=prophet (last access: 16 August 2018), 2018b.
Thornton, P. E., Thornton, M. M., Mayer, B. W., Wilhelmi, N., Wei, Y., Devarakonda, R., and Cook, R. B.: Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1219, 2014.
Tyralis, H. and Koutsoyiannis, D.: A Bayesian statistical model for deriving the predictive distribution of hydroclimatic variables, Clim. Dynam., 42, 2867–2883, https://doi.org/10.1007/s00382-013-1804-y, 2014.
Tyralis, H. and Papacharalampous, G.: Variable selection in time series forecasting using random forests, Algorithms, 10, https://doi.org/10.3390/a10040114, 2017.
Tyralis, H. and Papacharalampous, G. A.: Large-scale assessment of Prophet for multi-step ahead forecasting of monthly streamflow, Adv. Geosci., 45, 147–153, https://doi.org/10.5194/adgeo-45-147-2018, 2018.
Tyralis, H., Dimitriadis, P., Koutsoyiannis, D., O'Connell, P. E., Tzouka, K., and Iliopoulou, T.: On the long-range dependence properties of annual precipitation using a global network of instrumental measurements, Adv. Water Resour., 111, 301–318, https://doi.org/10.1016/j.advwatres.2017.11.010, 2018.
Verikas, A., Gelzinis, A., and Bacauskiene, M.: Mining data with random forests: A survey and results of new tests, Pattern Recogn., 44, 330–349, https://doi.org/10.1016/j.patcog.2010.08.011, 2011.
Warnes, G. R., Bolker, B., Gorjanc, G., Grothendieck, G., Korosec, A., Lumley, T., MacQueen, D., Magnusson, A., and Rogers, J.: gdata: Various R Programming Tools for Data Manipulation, R package version 2.18.0, available at: https://CRAN.R-project.org/package=gdata (last access: 16 August 2018), 2017.
Wickham, H.: ggplot2, Springer International Publishing, https://doi.org/10.1007/978-3-319-24277-4, 2016.
Wickham, H.: scales: Scale Functions for Visualization, R package version 1.0.0, available at: https://CRAN.R-project.org/package=scales (last access: 16 August 2018), 2018.
Wickham, H., Hester, J., and Francois, R.: readr: Read Rectangular Text Data, R package version 1.1.1, available at: https://CRAN.R-project.org/package=readr (last access: 16 August 2018), 2017.
Wickham, H, Chang, W., Henry, L., Pedersen, T. L., Takahashi, K., Wilke, C., and Woo, K.: ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics, R package version 3.0.0, available at: https://CRAN.R-project.org/package=ggplot2 (last access: 16 August 2018), 2018a.
Wickham, H., Hester, J., and Chang, W.: devtools: Tools to Make Developing R Packages Easier, R package version 1.13.6, available at: https://CRAN.R-project.org/package=devtools (last access: 16 August 2018), 2018b.
Wright, M. N.: ranger: A Fast Implementation of Random Forests, R package version 0.10.1, available at: https://CRAN.R-project.org/package=ranger (last access: 16 August 2018), 2018
Wright, M. N. and Ziegler, A.: ranger: A Fast Implementation of Random Forests for High Dimensional Data in C and R, J. Stat. Softw., 77, https://doi.org/10.18637/jss.v077.i01, 2017.
Wu, W., Dandy, G. C., and Maier, H. R.: Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling, Environ. Modell. Softw., 54, 108–127, https://doi.org/10.1016/j.envsoft.2013.12.016, 2014.
Xie, Y.: knitr: A Comprehensive Tool for Reproducible Research in R, in: Implementing Reproducible Computational Research, Chapman and Hall/CRC, 2014.
Xie, Y.: Dynamic Documents with R and knitr, 2nd edition, Chapman and Hall/CRC, 2015.
Xie, Y.: knitr: A General-Purpose Package for Dynamic Report Generation in R, R package version 1.20, available at: https://CRAN.R-project.org/package=knitr (last access: 16 August 2018), 2018.
Zeileis, A. and Grothendieck, G.: zoo: S3 infrastructure for regular and irregular time series, J. Stat. Softw., 14, https://doi.org/10.18637/jss.v014.i06, 2005.
Zeileis, A., Grothendieck, G., and Ryan, J. A.: zoo: S3 Infrastructure for Regular and Irregular Time Series (Z's Ordered Observations), R package version 1.8-3, available at: https://CRAN.R-project.org/package=zoo (last access: 16 August 2018), 2018.
Zhang, Z., Zhang, Q., and Singh, V. P.: Univariate streamflow forecasting using commonly used data-driven models: literature review and case study, Hydrolog. Sci. J., 63, 1091–1111, https://doi.org/10.1080/02626667.2018.1469756, 2018.